Рассмотрим примеры, в которых дан график функции, на котором отмечены точки. Нужно определить, в какой из этих точек значение производной наименьшее.
№1
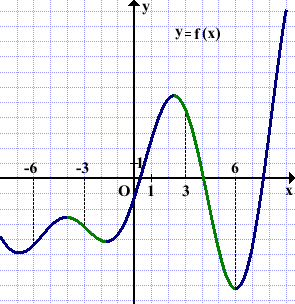
На рисунке изображён график функции y=f(x) и отмечены точки -6, -3, 3 и 6. В какой из этих точек значение производной наименьшее? В ответе указать эту точку.
 Решение:
Решение:
Точка x=6 — точка минимума функции y=f(x), поэтому производная в этой точке обращается в нуль: f'(6)=0.
Точка x=-6 принадлежит промежутку возрастания функции, поэтому производная в этой точке принимает положительное значение: f'(-6)>0.
Точки x=-3 и x=3 принадлежат промежуткам убывания функции, поэтому в этих точках значения производной отрицательны: f'(-3)<0 и f'(3)<0.
Остаётся сравнить f'(-3) и f'(3).
1 способ
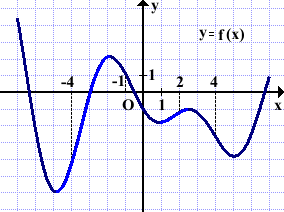 Решение:
Решение: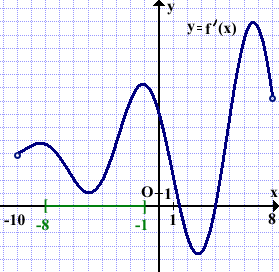 Решение:
Решение: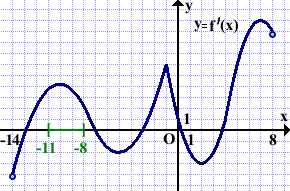 Выделяем отрезок [-11;-8].
Выделяем отрезок [-11;-8].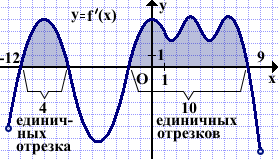 На промежутках возрастания функции y=f(x) её производная y=f'(x) положительна.
На промежутках возрастания функции y=f(x) её производная y=f'(x) положительна.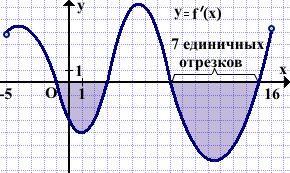 Решение:
Решение: