С помощью этой ассоциации легко запомнить формулу для решения частного случая простейшего тригонометрического уравнения cosx=-1.
Итак, снова ассоциация косинус-колобок.
Колобок движется влево-вправо, а не вверх вниз — его фигура предполагает именно такое движение. А вправо-влево у нас происходит движение по оси ox. Значит, косинус — это x.
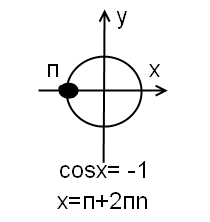
И когда нам надо решить уравнение cosx=-1, это означает, что требуется найти точки, в которых x равен -1.
Как и для других частных случаев косинуса, рассматриваем решение данного уравнения на единичной окружности, то есть на окружности с радиусом 1.
Так как cosx=-1, а косинус — это x, идем влево на 1. Попадаем в точку п. Это лишь одна из точек, в которых cosx=-1.
Таких точек — бесконечное множество. В каждую следующую точку попадаем через полный оборот окружности, то есть через 2п. Чтобы учесть все эти точки, 2п умножаем на n, где n — целое число.
Итак, решение уравнения cosx=-1 — это множество точек x=п+2пn, где n — целое число. Проиллюстрируем эти рассуждения рисунком:
решение уравнения cosx=-1