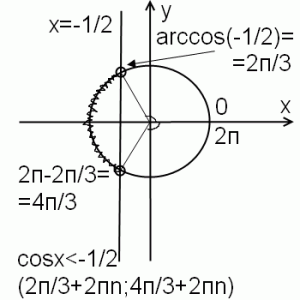Узнать ещё

Рассмотрим решение тригонометрических неравенств вида cosx меньше a (cosx<a) на единичной окружности.

Снова применяем ассоциацию косинус-колобок. Оба кругленькие, оба начинаются с ко-. Колобку, в силу особенности его фигуры, удобнее двигаться влево-вправо, а не вверх-вниз. Влево-вправо на координатной плоскости — движение по оси ox. Значит, косинус — это x. То есть абсцисса,  координата x точки на окружности. Геометрически cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси ox). Соответственно, точки окружности, находящиеся правее этой прямой, соответствуют значениям косинуса, большим a, а cosx меньше a — левее этой прямой. Прямая и окружность могут пересекаться, не пересекаться и касаться. От их взаимного расположения зависит решение тригонометрического неравенства cosx меньше a.

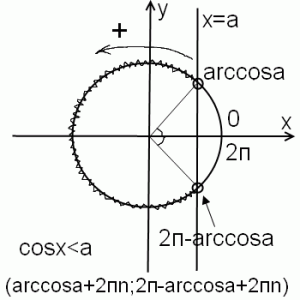
1) cosx<a, при 0<a<1.

 

Первая точка пересечения прямой и окружности находится, как обычно, — это arccos a. Поскольку нам нужны значения, в которых cos x меньше a, из первой точки ко второй мы идем по верхнему пути, против часовой стрелки. При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки.

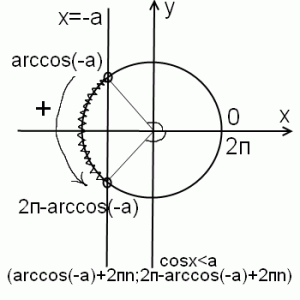
2) cos x меньше -a, при 0<a<1.

Решение неравенства аналогично первому случаю. Отличие — нужно вычислить арккосинус отрицательного числа (чуть позже я расскажу, как легко запомнить значения arccos (-a) с помощью ассоциации). А пока что arccos (-a)= п-arccos a. Ко второй точке здесь тоже идем против часовой стрелки, то есть значение угла увеличивается. Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой).

3) cosx<0

То есть ищем, где косинус отрицательный.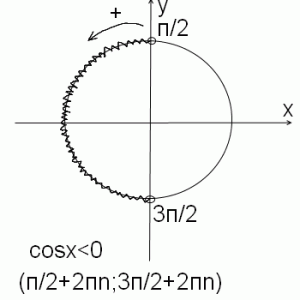

В качестве первой точки промежутка, на котором косинус принимает отрицательные значения, берем п/2, вторая точка — 3п/2. Чтобы учесть все промежутки, на которых косинус отрицательный, прибавляем к концам промежутка 2пn. Таким образом, решение тригонометрического неравенства cosx<0 есть промежуток (п/2+2пn; 3п/2+2пn), где n — целое число. Если неравенство нестрогое, то есть ищем неотрицательные значения косинуса, точки закрашиваем, скобки берем квадратные.

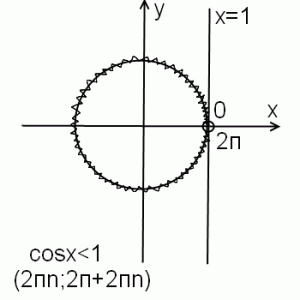
4) cosx<1

В этом случае окружность и прямая x=a касаются в одной точке — в нуле. Таким образом, за исключением этой точки, окружность расположена левее прямой. Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn. Получаем (2пn; 2п+2пn).

5) cosx<a, при a>1.

В этом случае окружность целиком лежит левее прямой x=a и любое значение x удовлетворяет условию неравенства. Таким образом, в этом случае косинус меньше a на промежутке (-∞;+∞).

6) cosx<-a, при a>1.

При таких a окружность целиком расположена правее прямой x=-a и нет ни одного x, удовлетворяющего требованию cosx меньше -a. Поэтому решений нет.

   

В этом случае точку пересечения окружности и прямой исключать из решения не нужно, значит, x — любое число и решением является вся числовая прямая: (-∞;+∞).

   

Единственным решением этого тригонометрического неравенства является точка п. С учетом периодичности косинуса, решением является множество точек вида п+2пn, где n — целое число.

И в заключении — пример решения тригонометрического неравенства вида cosx меньше a: cosx<-1/2: