« »

Рубрика: Запомнить? Легко!

Объем пирамиды

Используя это рассуждение, можно легко запомнить, как найти объем пирамиды, призмы, конуса и цилиндра.

Если обратить внимание на тот факт, что объем пирамиды, объем конуса, объем призмы и объем цилиндра вычисляются практически по одной и той же формуле, их можно легко запомнить и в дальнейшем без труда восстановить в памяти в любой ситуации, даже в стрессовых условиях экзамена или контрольной работы.

Объем цилиндра и объем призмы находятся по одной формуле

объем цилиндра, объем призмы

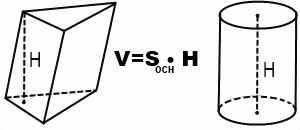
Объем пирамиды и объем конуса тоже находятся по одной формуле:

объем пирамиды, объем конуса

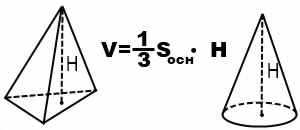
Отличие первой формулы от второй — появление у формулы для нахождения объема пирамиды и конуса коэффициента 1/3. То есть при одинаковых площадях основания и высотах объем пирамиды и объем конуса составляют третью часть от объемов призмы и цилиндра.

Осталось дополнить, что в основании конуса и цилиндра лежит круг, площадь круга —

    \[{S_{kp}} = \pi {R^2}.\]

Отсюда формула объема конуса

    \[{V_k} = \frac{1}{3}\pi {R^2}H\]

формула для нахождения объема цилиндра

    \[V = \pi {R^2}H\]

4 комментария , 12 Май 2013

4 комментария на «Объем пирамиды»

  1. Газиз:
    25.12.2013 в 1:58 пп

    Спасибо за такой хороший сайт. Очень много полезной информации.
    Буду советовать всем. (Привет из КЗ)

    Ответить
  2. Валентина:
    05.01.2015 в 8:57 дп

    Спасибо, Светлана! Благодаря Вам обновляю для дочери знания, полученные более 40 лет назад! Надеюсь, не последний раз, внуки подрастают…

    Ответить
    • Светлана Иванова:
      07.01.2015 в 7:30 пп

      Валентина, удачи Вам! Вот что значит хорошая школа! Надеюсь, дочь и внуки проникнутся пониманием ценности знаний.

      Ответить

Ваш отзыв