Пирамида вписана в конус, если основание пирамиды — многоугольник, вписанный в основание конуса. Вершина пирамиды совпадает с вершиной конуса. Боковые ребра вписанной пирамиды для конуса являются образующими. Соответственно, в этом случае конус описан около пирамиды.
Пирамиду можно вписать в конус, если около ее основания можно описать окружность (другой вариант — пирамида может быть вписана в конус, если все ее боковые ребра равны). Высоты вписанной пирамиды и конуса совпадают.
Если в конус вписана треугольная пирамида, расположение центра описанной окружности зависит от вида треугольника, лежащего в ее основании.
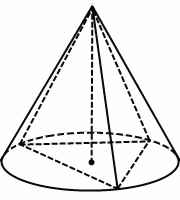
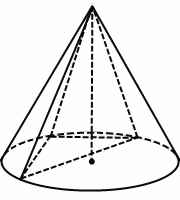
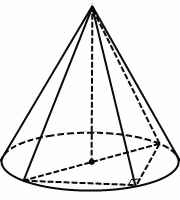
Если этот треугольник остроугольный, центр описанной около пирамиды окружности (а также основание высоты пирамиды и конуса) лежит внутри треугольника, если тупоугольный — вне его. Если в конус вписана прямоугольная пирамида, центр описанной окружности лежит на середине гипотенузы основания, то есть радиус описанного конуса равен половине гипотенузы. При этом высота конуса и цилиндра совпадает с высотой боковой грани, содержащей гипотенузу.
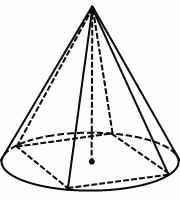
Четырехугольную пирамиду можно вписать в конус, если суммы противолежащих углов четырехугольника в основании равны по 180º (из параллелограммов это условие выполняется для прямоугольника и квадрата, из трапеций — только для равнобокой).
Найдем отношение объема вписанной пирамиды к объему конуса.
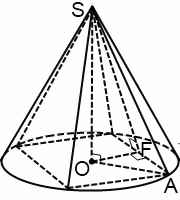Здесь SO=H — высота конуса и высота пирамиды, SA=l- образующая конуса, AO=R — радиус конуса(и радиус описанной около основания пирамиды окружности).
![\[\frac{{{V_n}}}{{{V_k}}} = \frac{{\frac{1}{3}{S_{ocn}}H}}{{\frac{1}{3}\pi {R^2}H}} = \frac{{{S_{ocn}}}}{{\pi {R^2}}}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-78710f928b2b8c9d3fdbe1d73d263542_l3.png "Rendered by QuickLaTeX.com")
Если в конус вписана правильная четырехугольная пирамида, получаем:
![\[\frac{{{V_n}}}{{{V_k}}} = \frac{{{a^2}}}{{\pi {R^2}}} = \frac{{{{(R\sqrt 2 )}^2}}}{{\pi {R^2}}} = \frac{{2{R^2}}}{{\pi {R^2}}} = \frac{2}{\pi }.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-11d7acd66dec59fdb519de32b8527312_l3.png "Rendered by QuickLaTeX.com")
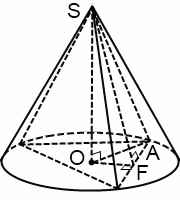
Если в конус вписана правильная треугольная пирамида:
![\[\frac{{{V_n}}}{{{V_k}}} = \frac{{\frac{{{a^2}\sqrt 3 }}{4}}}{{\pi {R^2}}} = \frac{{\frac{{{{(R\sqrt 3 )}^2}\sqrt 3 }}{4}}}{{\pi {R^2}}} = \frac{{3\sqrt 3 {R^2}}}{{4\pi {R^2}}} = \frac{{3\sqrt 3 }}{{4\pi }}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-cb9fe1e1a3a7b398e9e6c0cf2512fd6b_l3.png "Rendered by QuickLaTeX.com")
(Подсказка, как запомнить формулу правильного треугольника).
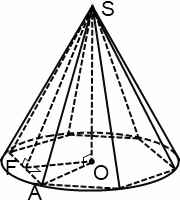Когда в конус вписана правильная шестиугольная пирамида, отношение объема пирамиды к объему конуса равно:
![\[\frac{{{V_n}}}{{{V_k}}} = \frac{{\frac{{3\sqrt 3 {a^2}}}{2}}}{{\pi {R^2}}} = \frac{{\frac{{3\sqrt 3 {R^2}}}{2}}}{{\pi {R^2}}} = \frac{{3\sqrt 3 }}{{2\pi }}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d504ced24eda5a5a9fe5de28dcaff0fa_l3.png "Rendered by QuickLaTeX.com")
(Подсказка, как запомнить формулу площади правильного шестиугольника).
Если в конус вписана правильная пирамида, проекцией ее апофемы на плоскость основания является радиус вписанной в основание окружности (на рисунках SF — апофема, OF=r). Таким образом, в зависимости от начальных данных, в ходе решения задачи на вписанную в конус пирамиду можно рассмотреть прямоугольный треугольник SOA либо SOF (или оба).