Узнать ещё

Среди задач на пирамиду правильная пирамида встречается чаще других. Чтобы легко решать такие задачи, нужно знать свойства правильной пирамиды.

Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.

Высота боковой грани, проведенная из вершины правильной пирамиды, называется апофемой.

 

 

 

 

 

 

 

 

 

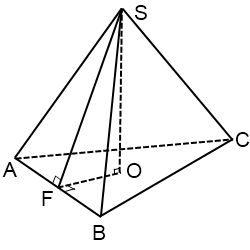
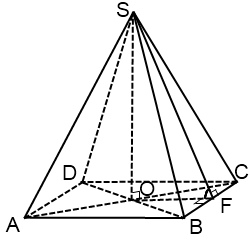
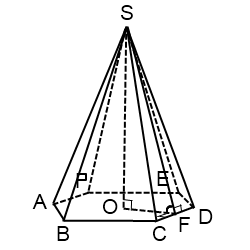
SF — апофема

   

— двугранный угол при основании пирамиды

SO — высота пирамиды

 

 

 

 

Свойства правильной пирамиды

— боковые ребра равны;

— боковые грани равны (все — равнобедренные треугольники);

— апофемы равны;

— двугранные углы при основании равны;

— боковые ребра одинаково наклонены к плоскости основания;

— основание высоты пирамиды является центром вписанной и описанной около основания окружностей;

— каждая точка высоты правильной пирамиды равноудалена от вершин основания;

— каждая точка высоты правильной пирамиды равноудалена от боковых граней;

— высота правильной пирамиды образует с апофемами равные углы.

Боковая поверхность правильной пирамиды

В правильной пирамиде основание является ортогональной проекцией боковой поверхности. Поэтому

   

где φ — двугранный угол при основании. Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле

   

Еще одна формула боковой поверхности правильной пирамиды:

   

где P — периметр основания, l — апофема пирамиды.