« »

Рубрика: Комбинации геометрических тел

Шар, вписанный в конус

Рассмотрим некоторые соотношения, которые полезны при решении задач на шар, вписанный в конус.

 

 

 

шар в конусе

 

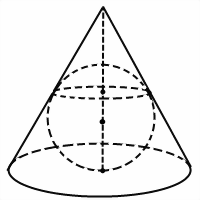
В любой конус можно вписать шар. Вписанный в конус шар (или сфера, вписанная в конус) касается основания конуса в его центре, а боковой поверхности — по окружности. Центр шара (сферы) лежит на оси конуса.

 

 

 

 

При решении задач на шар, вписанный в конус, удобнее всего рассмотреть сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара.

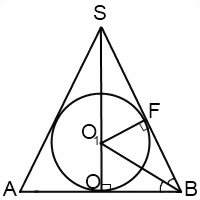осевое сечение комбинации "шар в конусе"Это сечение  представляет собой равнобедренный треугольник, боковые стороны которого — образующие конуса, а основание — диаметр конуса. Вписанный в этот треугольник круг — большой круг шара (то есть круг, радиус которого равен радиусу шара).

Для данного рисунка образующие SA=SB=l, высота конуса SO=H, радиус вписанного шара OO1=O1F=R. Так как центр вписанного круга — точка пересечения биссектрис треугольника, то ∠OBO1=∠FBO1, OB=r — радиус конуса.

Рассмотрим прямоугольный треугольник SOB. По свойству биссектрисы треугольника:

    \[\frac{{SB}}{{S{O_1}}} = \frac{{OB}}{{O{O_1}}}, \Rightarrow \frac{l}{{H - R}} = \frac{r}{R}\]

    \[lR = (H - R)r,lR = Hr - Rr,\]

    \[lR + Rr = Hr,R(l + r) = Hr,\]

    \[R = \frac{{Hr}}{{I + r}}.\]

По теореме Пифагора

    \[SB = \sqrt {S{O^2} + O{B^2}} , \Rightarrow l = \sqrt {{H^2} + {r^2}} \]

Отсюда

    \[\frac{{\sqrt {{H^2} + {r^2}} }}{{H - R}} = \frac{r}{R}.\]

Рассмотрим прямоугольный треугольник OO1B.

    \[O{O_1} = OB \cdot tg\angle OB{O_1}\]

Если ∠OBS=α, то ∠OBO1=α/2. Отсюда

    \[R = r \cdot tg\frac{\alpha }{2}.\]

Если сначала выразить радиус конуса через его высоту из прямоугольного треугольника SOB

    \[OB = SO \cdot ctg\alpha , \Rightarrow r = H \cdot ctg\alpha ,\]

то из треугольника OO1B выражаем радиус шара через высоту конуса:

    \[r = H \cdot ctg\alpha \cdot tg\frac{\alpha }{2}.\]

1 отзыв , 15 Фев 2013

Один отзыв на «Шар, вписанный в конус»

  1. София:
    09.02.2017 в 2:58 пп

    Спасибо за понятные объяснения и уроки)

    Ответить

Ваш отзыв