Хотя синус арккосинуса ( sin arccos x) несложно найти через тригонометрическую единицу, более простое и наглядное решение можно получить через геометрическую интерпретацию синуса и косинуса, определение арккосинуса и теорему Пифагора.
 По определению арккосинуса, если
По определению арккосинуса, если
![]()
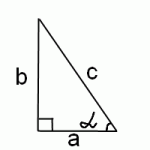
Но в прямоугольном треугольнике косинус равен отношению прилежащего катета к гипотенузе:
![]()
Нам нужен синус этого же угла альфа. А он равен отношению противолежащего катета к гипотенузе:
![]()
Противолежащий катет находим по теореме Пифагора:
![]()
Отсюда
![]()
где
![]()
Примеры
1) Найти sin (arccos (1/3)).
В этом примере x=1/3, отсюда прилежащий катет a=1, гипотенуза c=3. Находим противолежащий катет b:
![]()
Отсюда
![]()
2) Найти sin (arccos (3/5)) (или sin (arccos 0,6)).
Арккосинус трех пятых — это число, косинус которого равен 3/5. Косинус — отношение прилежащего катета к гипотенузе. Значит, прилежащий катет а=3, гипотенуза с=5. Отсюда противолежащий катет — 4. Синус — отношение противолежащего катета к гипотенузе. Отсюда
![]()
Я так понимаю, что формула для sin(arccos(x)) верна только для 0 <= x <= Pi/2. Для других x она не доказана
Даже для 0