Трапеция вписана в окружность

Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.

Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.

Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.

Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.

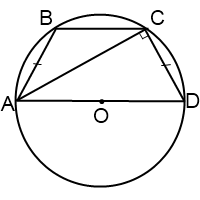трапеция в окружности Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:

$R = \frac{1}{2}AD$

центр окружности, описанной около трапеции

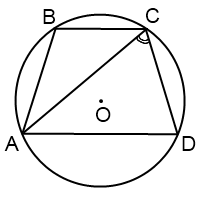
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.

центр окружности, описанной около трапеции

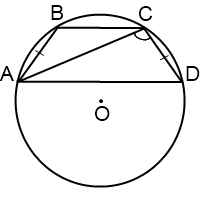
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.

Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD

$R = \frac{{AC}}{{2\sin \angle D}} = \frac{{CD}}{{2\sin \angle CAD}} = \frac{{AD}}{{2\sin \angle ACD}}$

Из треугольника ABC

$R = \frac{{AB}}{{2\sin \angle ACB}} = \frac{{BC}}{{2\sin \angle BAC}} = \frac{{AC}}{{2\sin \angle B}}$

Другой вариант найти радиус описанной окружности —

$R = \frac{{AC \cdot CD \cdot AD}}{{4{S_{ACD}}}}$

$R = \frac{{AB \cdot BC \cdot AC}}{{4{S_{ABC}}}}$

радиус описанной около трапеции окружности

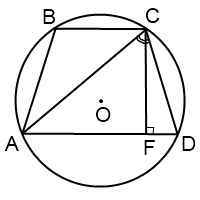
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:

$\sin \angle D = \frac{{CF}}{{CD}}$

$\sin \angle CAD = \frac{{CF}}{{AC}}$

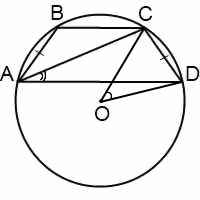окружность описана около трапеции При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,

$\angle CAD = \frac{1}{2}\angle COD$

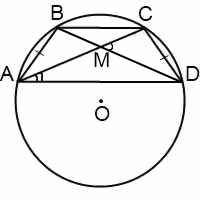Трапеция, вписанная в окружность Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали