Угловой коэффициент прямой

Угловой коэффициент прямой y=kx+b равен k.

Почему число k называется угловым коэффициентом?

Графиком линейной функции y=kx+b является прямая. С положительным направлением оси абсцисс эта прямая составляет угол α.

Утверждение:

Угловой коэффициент прямой равен тангенсу угла между прямой и положительным направлением оси абсцисс.

Доказательство:

I. Если угол между прямой и положительным направлением оси абсцисс острый.

Выберем на прямой y=kx+b две точки A(x₁;y₁) и B(x₂;y₂).

Их координаты удовлетворяют уравнению прямой, поэтому y₁=kx₁+b и y₂=kx₂+b.

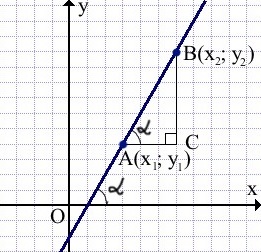uglovoj-koehfficient Вычтем почленно первое равенство из второго:

$- \frac{\begin{array}{l} y_2 = kx_2 - b \\ y_1 = kx_1 - b \\ \end{array}}{{y_2 - y_1 = kx_2 - kx_1 }}$

откуда y₂-y₁=k(x₂-x₁) и

$k = \frac{{y_2 - y_1 }}{{x_2 - x_1 }}.$

y₂-y₁=BC, x₂-x₁=AC,

$\frac{{BC}}{{AC}} = tg\alpha .$

Таким образом, k=tgα.

II. Если угол между прямой и положительным направлением оси абсцисс тупой.

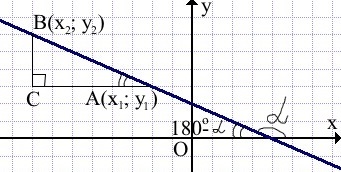
uglovoj-koehfficient-pryamoj

В этом случае

$k = \frac{{y_2 - y_1 }}{{x_2 - x_1 }},$

$\frac{{y_2 - y_1 }}{{x_2 - x_1 }} = \frac{{BC}}{{AC}},$

$\frac{{BC}}{{AC}} = tg(180^o - \alpha ),$

$tg(180^o - \alpha ) = - tg\alpha ,$

$k = - tg\alpha .$

Таким образом, коэффициент k в уравнении прямой y=kx+b с точностью до знака равен тангенсу острого угла , который прямая образует с осью Ox.

Узнать ещё