Когда в задаче дана вписанная в шар пирамида, при ее решении будет полезна следующая теоретическая информация.
Если пирамида вписана в шар, то все ее вершины лежат на поверхности этого шара (на сфере), соответственно, расстояния от центра шара до вершин равны радиусу шара.
Каждая грань вписанной в шар пирамиды является вписанным в некоторую окружность многоугольником. Основания перпендикуляров, опущенных из центра шара на плоскости граней, являются центрами этих описанных окружностей. Таким образом, центр описанного около пирамиды шара — точка пересечения перпендикуляров к граням пирамиды, проведенных через центры описанных около граней окружностей.
Чаще центр описанного около пирамиды шара рассматривают как точку пересечения перпендикуляра, проведенного к основанию через центр описанной около основания окружности, и серединного перпендикуляра к боковому ребру (серединный перпендикуляр лежит в плоскости, проходящей через это боковое ребро и первый перпендикуляр (проведенный к основанию). Если около основания пирамиды нельзя описать окружность, то эта пирамида не может быть вписана в шар. Отсюда следует, что около треугольной пирамиды всегда можно описать шар, а вписанная в шар четырехугольная пирамида с параллелограммом в основании может иметь основанием прямоугольник либо квадрат.
Центр описанного около пирамиды шара может лежать внутри пирамиды, на поверхности пирамиды (на боковой грани, на основании), и вне пирамиды. Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.
Около любой правильной пирамиды можно описать шар. Его центр — точка пересечения прямой, содержащей высоту пирамиды, и серединного перпендикуляра к боковому ребру.
При решении задач на вписанную в шар пирамиду чаще всего рассматривают некоторые треугольники.
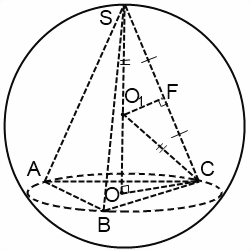
Начнем с треугольника SO1C. Он равнобедренный, поскольку две его стороны равны как радиусы шара: SO1=O1С=R. Следовательно, O1F — его высота, медиана и биссектриса.
Прямоугольные треугольники SOC и SFO1 подобны по острому углу S. Отсюда
![]()
SO=H — высота пирамиды, SC=b — длина бокового ребра, SF=b/2, SO1=R, OC=r — радиус окружности, описанной около основания пирамиды.
![]()
![]()
В прямоугольном треугольнике OO1C г гипотенуза O1C=R, катеты OC=r, OO1=H-R. По теореме Пифагора:
![]()
![]()
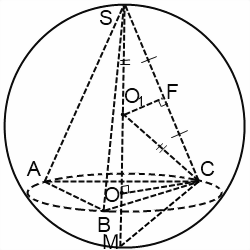
Если продолжить высоту SO, получим диаметр SM. Треугольник SCM — прямоугольный (так как вписанный угол SCM опирается на диаметр). В нем OC — высота, проведенная к гипотенузе, SO и OM — проекции катетов SC и CM на гипотенузу. По свойствам прямоугольного треугольника,
![]()
и еще раз, только другим путем:
![]()
Эти рассуждения верны не только для правильной пирамиды, но также для пирамиды, основание высоты которой является центром описанной около основания пирамиды окружности.
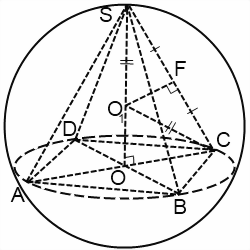
Добрый день! Не соглашусь с утверждением, что «вписанная в шар четырехугольная пирамида в основании имеет прямоугольник или квадрат»…Около равнобедренной трапеции тоже можно описать окружность…есть и другие виды 4-угольников (с равными суммами противоположных углов)
Да, Вы правы. Я неточно сформулировала свою мысль. Подкорректировала.