Задачи на цену, количество, стоимость начинают изучать еще в курсе математики начальной школы. В курсе алгебры решение задач на цену, как правило, проводится с помощью систем уравнений. Рассмотрим, как решать задачи на цену, количество, стоимость, на конкретном примере.
Цена, количество и стоимость связаны между собой соотношением:
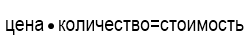
Условие задач на цену, количество, стоимость удобно оформлять в виде таблицы.
За 5 кг конфет и 4 кг печенья заплатили 1240 рублей. Сколько стоит 1 кг конфет и сколько стоит 1 кг печенья, если 3 кг конфет дороже, чем 2 кг печенья, на 304 рубля?
Решение:
Пусть цена 1 кг печенья x рублей, а 1 кг конфет — y рублей.
Составим и решим систему уравнений:
![\[\left\{ \begin{array}{l}4x + 5y = 1240\\3y - 2x = 304\end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-e1ddd92f1ca0ab1d6459184940d469a9_l3.png "Rendered by QuickLaTeX.com")
![\[\left\{ \begin{array}{l}4x + 5y = 1240\\ - 2x + 3y = 304\_\_\_\left| { \cdot 2} \right.\end{array} \right. \Rightarrow \left\{ \begin{array}{l}4x + 5y = 1240\\ - 4x + 6y = 608\end{array} \right.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-7e2dee373b5dd0da71d2192df1f8831c_l3.png "Rendered by QuickLaTeX.com")
Сложив уравнения почленно, получаем:
![\[11y = 1848, \Rightarrow y = 168.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ed72d32fa35f244f1c60a7f7f83307d2_l3.png "Rendered by QuickLaTeX.com")
Подставив найденное значение y во второе уравнение, имеем:
![\[3 \cdot 168 - 2x = 304, \Rightarrow x = 100.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-074beb50ad0513a60c72cd155e9dde6e_l3.png "Rendered by QuickLaTeX.com")
Значит, цена 1 кг печенья — 100 рублей, цена 1 кг конфет — 168 рублей.
Ответ: 168 руб. и 100 руб.
В следующий раз рассмотрим задачи, в которых речь идет об изменении цены.