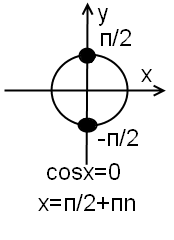Эта ассоциация помогает легко запомнить формулу для решения тригонометрического уравнения cosx=0.
Используем ассоциацию косинус-колобок.
Начинаются они одинаково, на ко-. Колобок движется влево-вправо, в силу особенностей своей фигуры. А влево-вправо на координатной плоскости происходит движение вдоль оси ox. Значит косинус — это x.
Для решения уравнения cosx=0 нам нужно найти точки, в которых косинус обращается в нуль. Как и в других частных случаях косинуса, решение ищем на единичной окружности, то есть на окружности с радиусом R=1.
Итак, cosx=0, косинус — это x, значит, двигаться ни влево, ни вправо не надо (колобок подпрыгнул на месте:)).
На единичной окружности x=0 соответствуют две точки: одна вверху, это п/2, другая — внизу, -п/2. Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть п.
Но через каждый интервал длиной п мы будет получать все новые и новые точки, в которых косинус равен нулю.
Чтобы учесть все такие точки, к первой точке прибавляем пn, где n — целое число (то есть принадлежит Z).
Таким образом, решение уравнения cosx=0 есть множество точек x=п/2+пn, где n — целое число. И соответствующий чертеж для иллюстрации ассоциации: