Рассмотрим одну из базовых задач планиметрии — биссектриса угла параллелограмма делит противолежащую сторону на отрезки.
Утверждение.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
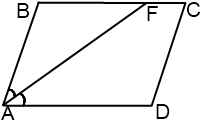
Пусть биссектриса угла A параллелограмма ABCD делит противолежащую сторону на отрезки BF=m, FC=n. Тогда:
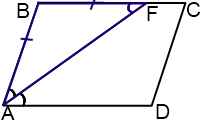 1)∠BAF=∠FAD
1)∠BAF=∠FAD
(так как AF — биссектриса угла A по условию);
2) ∠BFA=∠FAD (как внутренние накрест лежащие при AD ∥ BC и секущей AF);
3) следовательно, ∠BAF=∠BFA;
4) следовательно, треугольник ABF — равнобедренный (по признаку);
5) следовательно, AB=BF=m.
Этот рисунок иллюстрирует случай, когда дана биссектриса острого угла параллелограмма.
Если в задаче сказано, что биссектриса тупого угла параллелограмма делит сторону на отрезки, рассуждения аналогичны.
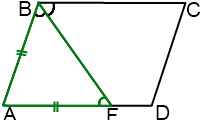
На базе этой задачи существует много других задач. Например: биссектриса угла A параллелограмма ABCD делит противолежащую сторону BC на отрезки BF=m, FC=n. Найти периметр параллелограмма.
После доказательства того, что AB=BF=m, нахождение периметра не вызывает затруднений: P=2(AB+BC)=2(m+m+n).
Замечательно! Просто и доходчиво:-)
Спасибо! 🙂
Как найти FC?
FC=BC-BF, а так как BF=AB, то FC=BC-AB.
Таким образом, биссектриса угла параллелограмма делит противоположную сторону на два отрезка, один из которых равен второй стороне параллелограмма, а другой — разности длин сторон параллелограмма.