« »

Рубрика: Задачи по планиметрии

Биссектриса в прямоугольном треугольнике

Рассмотрим задачу, в которой биссектриса в прямоугольном треугольнике делит катет (либо гипотенузу) на отрезки. Ее решение опирается на свойство биссектрисы треугольника и теорему Пифагора.

биссектриса впрямоугольного треугольника

 

 

Задача.

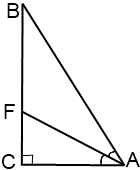
В прямоугольном треугольнике биссектриса острого угла делит катет на отрезки m и n. Найти периметр и площадь этого треугольника.

 

Решение:

Пусть в треугольнике ABC угол С — прямой, AF — биссектриса, BF=m, CF=n (m>n!).

По свойству биссектрисы треугольника,

    \[\frac{{AB}}{{BF}} = \frac{{AC}}{{CF}}.\]

Так как треугольник прямоугольный, по теореме Пифагора:

    \[A{B^2} = A{C^2} + B{C^2}.\]

Получили систему уравнений:

    \[\left\{ \begin{array}{l}\frac{{AB}}{{BF}} = \frac{{AC}}{{CF}};\\A{B^2} = A{C^2} + B{C^2}.\end{array} \right.\]

Пусть AB=x. AC=y (x>0, y>0). Тогда

    \[\left\{ \begin{array}{l}\frac{x}{m} = \frac{y}{n};\\{x^2} = {y^2} + {(m + n)^2}.\end{array} \right.\]

Выразим из первого уравнения одну переменную через другую и подставим полученное выражение во второе уравнение:

    \[y = \frac{{nx}}{m}, \Rightarrow {x^2} = \frac{{{n^2}}}{{{m^2}}}{x^2} + {(m + n)^2}\]

    \[{x^2} - \frac{{{n^2}}}{{{m^2}}}{x^2} = {(m + n)^2}\]

    \[(1 - \frac{{{n^2}}}{{{m^2}}}){x^2} = {(m + n)^2}\]

    \[\frac{{{m^2} - {n^2}}}{{{m^2}}} \cdot {x^2} = {(m + n)^2}\]

Извлекаем квадратный корень из обеих частей уравнения (это можно сделать, поскольку обе части положительны)

    \[\frac{{\sqrt {{m^2} - {n^2}} }}{m} \cdot x = m + n\]

и находим x и y, а значит, и AB и AC.

Периметр треугольника ABC равен P=AB+BC+AC, площадь —

    \[S = \frac{1}{2}AC \cdot BC.\]

Если биссектриса в прямоугольном треугольнике проведена не из острого, а из прямого угла, решение задачи аналогично.

Эта задача — базовая. Другие задачи, решение которых опирается на задачу о биссектрисе в прямоугольном треугольнике, разберем позже.

 

Ваш отзыв , 18 Апр 2013

Ваш отзыв