Узнать ещё

Если диагональ трапеции делит среднюю линию на отрезки, решение задачи сводится к рассмотрению двух треугольников.

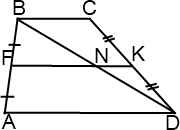
Пусть, для определенности, диагональ трапеции делит среднюю линию FK на отрезки FN=m, NK=n.

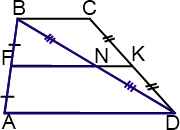
Рассмотрим треугольник ABD. Так как FK — средняя линия трапеции ABCD,

FN ∥ AD и FA=FB.Тогда по теореме Фалеса ND=NB. Отсюда FN — средняя линия треугольника ABD. По свойству средней линии треугольника:

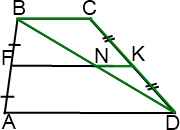Аналогично, в треугольнике BCD NK — средняя линия, а значит,