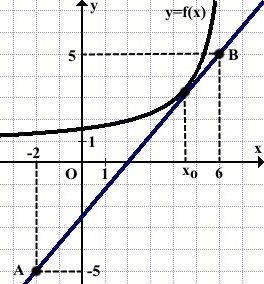
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой xо. Найти значение производной функции y=f'(x)в точке xо.
 №1
№1
Решение:
1-й способ
Значение производной y=f'(x) в точке xо равно угловому коэффициенту касательной к графику функции y=f(x) в точке xо:
f'(xо)=k.
На графике касательной ищем две выделенные точки с целыми координатами (иногда координаты этих точек уже подписаны):
A(-2;-5), B(6;5).
Уравнение прямой имеет вид y=kx+b.
Так как эта прямая проходит через точки A(-2;-5) и B(6;5), то их координаты удовлетворяют уравнению прямой.
Подставляем координаты A и B в уравнение прямой и из полученной системы уравнений находим k (для этого достаточно одно из уравнений системы умножить на -1 и сложить с другим уравнением).
![]()
![Rendered by QuickLaTeX.com \[ + \frac{{\left\{ \begin{array}{l} 5 = 2k - b \\ 5 = 6k + b \\ \end{array} \right.}}{{10 = 8k}} \]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-09c60c77658aad4fe792801dcdab27e2_l3.png)
k=1,25.
Следовательно, f'(xо)=1,25.
Ответ: 1,25.
2-й способ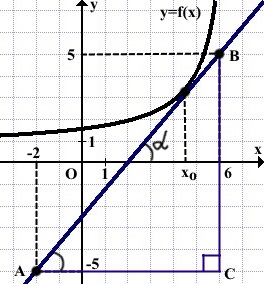
Значение производной y=f'(x) в точке xо равно тангенсу угла, который касательная, проведенная в точке xо, составляет с положительным направлением оси абсцисс:
f'(xо)=tgα.
Построим прямоугольный треугольник с вершинами в точках A и B.
∠BAC=α,
![]()
![]()
Значит, f'(xо)=1,25.
№2
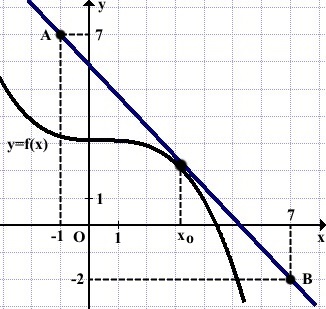 1-й способ:
1-й способ:
Точки с выделенными целыми координатами — A(-1;7) и B (7;-2).
Подставляем их координаты в уравнение прямой y=kx+b и находим из полученной системы уравнений коэффициент k:
![]()
![Rendered by QuickLaTeX.com \[ + \frac{{\left\{ \begin{array}{l} - 7 = k - b \\ - 2 = 7k + b \\ \end{array} \right.}}{{ - 9 = 8k}} \]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-eb0a2d044ed391c73a60ae50747ef659_l3.png)
k=-1,125.
f'(xо)=k=-1,125.
2-й способ:
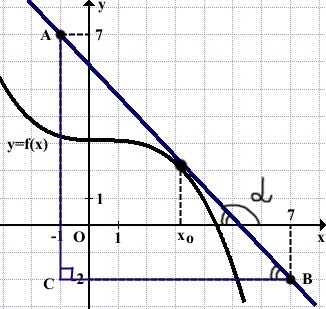 Строим прямоугольный треугольник ABC.
Строим прямоугольный треугольник ABC.
![]()
![]()
tgα=tg(180°-∠ABC)=-tg∠ABC,
tgα=-1,125.
f'(xо)=tgα=-1,125.
Ответ: -1,125.
№3
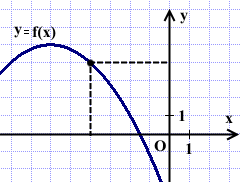 На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой -4. Найдите f'(-4).
На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой -4. Найдите f'(-4).
Решение:
f'(x)=k.
Так как касательная к графику функции проходит через начало координат, то уравнение касательной имеет вид y=kx.
Касательная проходит через точку (-4;4). Подставив координаты точки в уравнение касательной: 4=k·(-4), получаем k=-1.
Следовательно, f'(x)=-1.
Ответ: -1.