« »

Рубрика: Виды пирамид

Пирамиды, в которых грани перпендикулярны основанию

Рассмотрим, какими свойствами обладают пирамиды, в которых  боковые грани перпендикулярны основанию.

Если две смежные боковые грани пирамиды перпендикулярны основанию, то общее боковое ребро этих граней является высотой пирамиды. Если в задаче сказано, что ребро пирамиды является ее высотой, то речь идет именно об этом виде пирамид.

Грани пирамиды, перпендикулярные основанию — прямоугольные треугольники.

 

Если основание пирамиды — треугольник

боковые грани пирамиды перпендикулярны основанию

Боковую поверхность такой пирамиды в общем случае ищем как сумму площадей всех боковых граней.

Основание пирамиды является ортогональной проекцией грани, не перпендикулярной основанию (в данном случае, SBC). А значит, по теореме о площади ортогональной проекции, площадь основания равна произведению площади этой грани на косинус угла между нею и плоскостью основания.

 

 

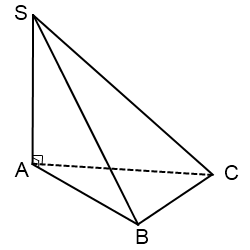
Если основание пирамиды — прямоугольный треугольник

грани пирамиды - прямоугольные треугольники

 

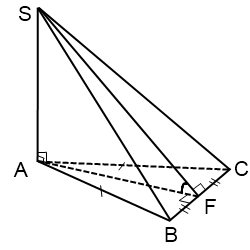
В этом случае все грани  пирамиды — прямоугольные треугольники.

Треугольники SAB и SAС прямоугольные, так как SA — высота пирамиды. Треугольник ABC прямоугольный по условию.

То, что треугольник SBC прямоугольный, следует из теоремы о трех перпендикулярах (AB — проекция наклонной SB на плоскость основания. Так как AB перпендикулярна BC по условию, то и SB перпендикулярна BC).

Угол между боковой гранью SBC и основанием в этом случае — угол ABS.

    \[{S_\Delta }_{ABC} = {S_\Delta }_{SBC} \cdot \cos \angle ABS\]

Площадь боковой поверхности равна сумме площадей прямоугольных треугольников:

    \[{S_{bok}} = {S_{ABS}} + {S_{BCS}} + {S_{ACS}}\]

Так как в данном случае

    \[BS = \frac{{AS}}{{\sin \angle ABS}}\]

    \[{S_{bok}} = \frac{1}{2}AS(AB + AC + \frac{{BC}}{{\sin \angle ABS}})\]

 

Если основание пирамиды — равнобедренный треугольник

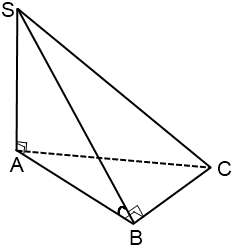
основание пирамиды - равнобедренный треугольник

В этом случае угол между плоскостью боковой грани BCS и плоскостью основания — это угол AFS, где AF — высота, медиана и биссектриса равнобедренного треугольника ABC.

Аналогично — если в основании пирамиды лежит равносторонний треугольник ABC.

 

 

    \[{S_\Delta }_{ABC} = {S_\Delta }_{SBC} \cdot \cos \angle AFS\]

 

 

Если основание пирамиды — параллелограмм

основание пирамиды - параллелограмм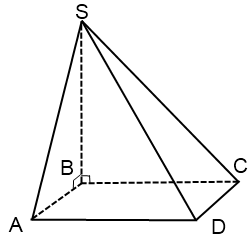В этом случае основание пирамиды является ортогональной проекцией боковых граней, не перпендикулярных основанию.

Если разбить основание на два треугольника, то

    \[{S_{\Delta ABD}} = {S_{\Delta ADS}}\cdot\cos \alpha ,\]

    \[{S_{\Delta BCD}} = {S_{CDS}}\cdot\cos \beta \]

где α и β — соответственно углы между плоскостями ADS и CDS и плоскостью основания.

 

 

основание пирамиды - параллелограмм

Если BF и BK — высоты параллелограмма, то угол BFS — это угол наклона боковой грани CDS к плоскости основания, а угол BKS — угол наклона грани ADS.

(чертеж сделан для случая, когда B — тупой угол).

Если в основании пирамиды лежит ромб ABCD, то углы BFS и BKS равны. Треугольники ABS и CBS, а также ADS и CDS в этом случае также равны.

 

 

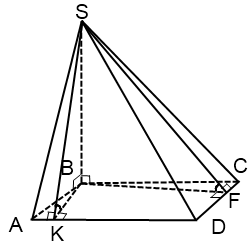
Если основание пирамиды — прямоугольник

основание пирамиды - прямоугольник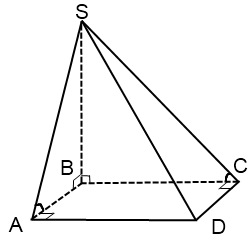В этом случае угол между плоскостью боковой грани SAD и плоскостью основания есть угол SAB,

а угол между плоскостью боковой грани SCD и плоскостью основания — угол SCB

(по теореме о трех перпендикулярах).

 

Соответственно,

 

 

 

    \[{S_{ocn}} = {S_{SAD}} \cdot \cos \angle SAB + {S_{SCD}} \cdot \cos \angle SCB\]

    \[{S_{\Delta ABD}} = {S_{\Delta ADS}} \cdot \cos \angle SAB,{S_{\Delta BCD}} = {S_{CDS}} \cdot \cos \angle SCB\]

Отсюда боковую поверхность можно найти как

    \[{S_{bok}} = {S_{\Delta ABS}} + {S_{\Delta BCS}} + \frac{{{S_{\Delta ABD}}}}{{\cos \angle SAB}} + \frac{{{S_{\Delta BCD}}}}{{\cos \angle SBC}}\]

Здесь все боковые грани пирамиды — прямоугольные треугольники (углы SAD и SCD прямые по теореме о трех перпендикулярах). Поэтому боковую поверхность можно искать непосредственно:

    \[{S_{bok}} = {S_{\Delta ABS}} + {S_{\Delta BCS}} + {S_{\Delta CDS}} + {S_{\Delta ADS}}\]

    \[{S_{bok}} = \frac{1}{2}(AB \cdot BS + BC \cdot BS + CD \cdot CS + AD \cdot AS)\]

Если в основании пирамиды лежит квадрат ABCD, то задача упрощается: треугольники ABS и BCS, а также треугольники ADS и CDS в этом случае равны.

 

 

 

12 комментариев , 15 Дек 2012

12 комментариев на «Пирамиды, в которых грани перпендикулярны основанию»

  1. Наталья:
    18.01.2015 в 12:50 пп

    Не согласна с определением прямоугольной пирамиды. Прямоугольная пирамида — это пирамида, в одной вершине из которых прилежат три прямых угла. Напишите мне, почему вы распрастраняете ошибочный материал на уровне невежественной википедии.

    Ответить
    • Светлана Иванова:
      18.01.2015 в 6:20 пп

      Наталья, а где Вы увидели «определение прямоугольной пирамиды»?

      Ответить
      • Natashok:
        20.01.2015 в 11:06 дп

        Если на русском языке гуглить «прямоугольная пирамида», то Ваш материал находится в пятерке. Я вижу, что на этой страничке только одна прямоугольная пирамида, последняя и то, обозначения не до конца корректны. Гугль вообще вместе с википедией странное определение выдал — перпендикулярное ребро и все равно, что в основании у пирамиды. Кстати на английском языке вообще прямоугольная пирамида -это пирамида, в основании которого находится прямоугольник и не важно где высота вообще.

        Ответить
        • Светлана Иванова:
          28.01.2015 в 9:14 пп

          В тексте о прямоугольной пирамиде нет ни слова. Очень часто в задачах на пирамиды, в которых есть две боковые грани, перпендикулярные основанию, речь идёт об угле между плоскостью боковой грани и плоскостью основания.
          В данном материале рассматриваются, как определить этот угол, в зависимости от многоугольника в основании. Если в основании лежит параллелограмм (в том числе, ромб), нужно из основания высоты пирамиды провести высоты параллелограмма к противоположным сторонам (или прямым, содержащим эти стороны). Если в основании — прямоугольник (в том числе, квадрат), высоты проводить не нужно, поскольку стороны прямоугольника взаимно перпендикулярны. В этом случае угол между основанием и боковой гранью определяется линейным углом, образованным ребрами пирамиды; боковые грани являются прямоугольными треугольниками.
          Прямые углы в основании выделены, чтобы подчеркнуть это отличие от случая, когда в основании лежит параллелограмм, не являющийся прямоугольником.

          Ответить
          • Наташок:
            21.04.2015 в 12:11 пп

            Потому что вы удалили «прямоугольная пирамида», но технарей, знающие и понимающие принцип работы поисковиков врядли может убедить ваши аргументы. Учите ИТ, а не только математику.

          • Светлана Иванова:
            27.04.2015 в 11:41 дп

            Уважаемая Наташок! Вы обвиняете меня во лжи? Я Вам сказала, что термин «прямоугольная пирамида» в своей работе не использую.
            P.S. Я не специалист в IT, увы. Согласна, грамотность нужна во всех областях: и в математике, и в информационных технологиях, и в правописании.

  2. NATASHOK:
    18.01.2015 в 3:52 пп

    Если в основании пирамиды прямоугольник, то почему для его обозначения на картинке отмечено два противополжных угла? На последнем чертеже это основание может быть ромбоидом и другим четырехугольником.

    Ответить
    • Светлана Иванова:
      18.01.2015 в 6:29 пп

      Рисунок иллюстрирует случай, когда в основании пирамиды лежит прямоугольник. При параллельном проектировании углы не сохраняются, поэтому прямоугольник изображается в виде параллелограмма. Второй прямой угол на рисунке отмечен в связи с теоремой о трёх перпендикулярах.

      Ответить
      • Natashok:
        20.01.2015 в 11:13 дп

        Во-первых не рисунок, а чертеж. Рисунки Вы оформляете на рисовании, а в математике все-таки чертежи. Во вторых посмотрите на последний чертеж. Там нет никаких теорем о трех перпендикулярах. Основание на последнем чертеже повторю не прямоугольник. Здесь не важно, как его Вы изобразите. Я слежу за обозначениями. Хотя я обратила внимание, что и снизу третий чертеж для меня не понятен. Параллелограмм не отмечен на чертеже. Просто четырехугольник! Его вид да похож на параллелограмм, но обозначения оставляют желать лучшее.

        Ответить
        • Светлана Иванова:
          28.01.2015 в 9:30 пп

          1) Да, в геометрии мы выполняем чертеж, но иллюстрация к тексту — рисунок. В любом учебнике по геометрии пишут «на рисунке 1», а не «на чертеже 1».
          2) Прямоугольник в стереометрии изображается параллелограммом, поскольку при параллельном проектировании углы не сохраняются. А вот параллельность прямых — сохраняется. Противолежащие стороны четырёхугольника изображены лежащими на параллельных прямых. Из этого следует, что этот четырёхугольник — параллелограмм.

          Ответить
          • Наташок:
            21.04.2015 в 12:08 пп

            Противолежащие стороны четырёхугольника изображены лежащими на параллельных прямых. Я не вижу обозначений, что эти прямые параллельны и в тексте не было указано о параллельном проектировании. Так что для меня основание все-таки на последнем чертеже произвольный четырехугольник

          • Светлана Иванова:
            27.04.2015 в 11:24 дп

            Уважаема Наташок! Изображение пространственных фигур на плоскости ведётся в соответствии с правилами параллельного проектирование. Это означает, что параллельные прямые на чертеже изображаются параллельными прямыми, а не параллельные — не параллельными.

Ваш отзыв