Узнать ещё

Как определить точки экстремума на графике функции?

Точки экстремума — это точки минимума и точки максимума функции.

Точка x_o называется точкой минимума функции f(x), если для любого x из некоторой окрестности x_o выполняется неравенство f(x_o)<f(x).

Примеры точек минимума на графике функции.

 

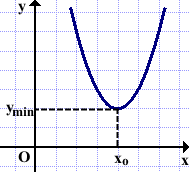
1)Точка минимума x_o имеет вид гладкой «впадины».

Производная в такой точке равна нулю:

f'(x_o)=0

Касательная к графику функции, проведённая в точке x_o, параллельна оси абсцисс.

 

 

 

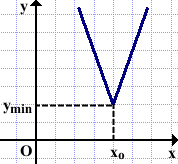
2)Точка минимума x_o имеет вид заострённой «впадины».

Производная в такой точке не существует.

Касательной к графику функции в точке x_o не существует.

 

 

 

 

 

 

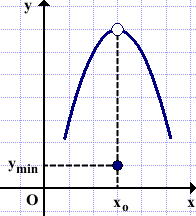
3) Точка минимума x_o — изолированная точка графика.

Функция в этой точке не является непрерывной (x_o — точка разрыва).

 

 

 

 

 

 

Точка x_o называется точкой максимума функции f(x), если для любого x из некоторой окрестности x_o выполняется неравенство f(x_o)>f(x).

 

Примеры точек максимума на графике функции.

 

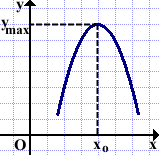
1)Точка максимума x_o имеет вид гладкого «холма».

Производная в такой точке равна нулю:

f'(x_o)=0

Касательная к графику функции, проведённая в точке x_o, параллельна оси абсцисс.

 

 

 

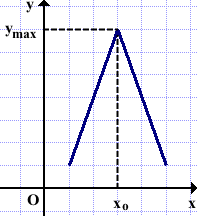
2)Точка максимума x_o имеет вид заострённой «вершины».

Производная в такой точке не существует.

Касательной к графику функции в точке x_o не существует.

 

 

 

 

 

 

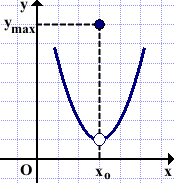
3) Точка максимума x_o — изолированная точка графика.

Функция в этой точке не является непрерывной.

 

 

 

 

И ещё один пример на нахождение точек экстремума по графику функции.

На рисунке дан график функции y=f(x).

Функция имеет 6 точек экстремума.

 

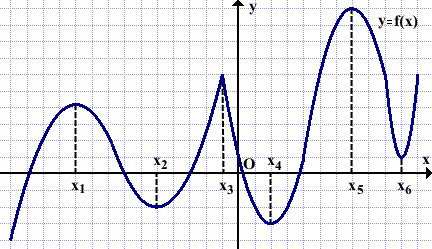
x₂, x₄ , x₆ — точки минимума функции y=f(x).

x₁, x₃, x₅ — точки максимума функции y=f(x).

Точки экстремума функции y=f(x) на графике её производной y=f'(x) ищем иначе!