« »

Рубрика: Комбинации геометрических тел

Цилиндр вписан в конус

Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.

цилиндр в конусе

 

 

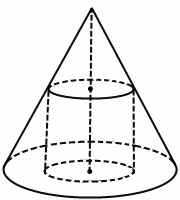
Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.

 

 

Рассмотрим осевое сечение комбинации тел. Оно представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

цилиндр, вписанный в конус

сечение цилиндра в конусе

 

 

 

 

 

 

 

 

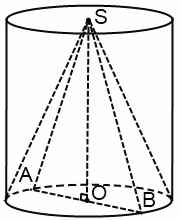
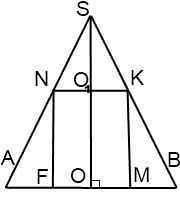
Здесь SO=H — высота конуса, OA=OB=R — радиус конуса, OF=OM=r — радиус цилиндра, OO1=h — высота цилиндра, SA=SB=l — образующие конуса, NF=KM=h — образующие цилиндра.

Прямоугольные треугольники SOB и KMB подобны (по общему острому углу B). Из подобия треугольников следует пропорциональность соответствующих сторон:

    \[\frac{{SO}}{{KM}} = \frac{{OB}}{{MB}}, \Rightarrow \frac{H}{h} = \frac{R}{{R - r}}.\]

Найдем отношение объемов конуса и вписанного в него цилиндра:

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}\pi {R^2}H}}{{\pi {r^2}h}} = \frac{1}{3} \cdot \frac{{{R^2}}}{{{r^2}}} \cdot \frac{H}{h}\]

С учетом предыдущего соотношения для высот конуса и цилиндра, имеем:

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{1}{3} \cdot \frac{{{R^2}}}{{{r^2}}} \cdot \frac{R}{{R - r}} = \frac{{{R^3}}}{{3{r^2}(R - r)}}.\]

Найдем отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра:

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{\pi Rl}}{{2\pi rh}} = \frac{{Rl}}{{2rh}}\]

Из прямоугольного треугольника SOB по теореме Пифагора 

    \[S{B^2} = O{B^2} + S{O^2}, \Rightarrow l = \sqrt {{R^2} + {H^2}} \]

Таким образом, 

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{R\sqrt {{R^2} + {H^2}} }}{{2rh}}.\]

Ваш отзыв , 12 Мар 2013

Ваш отзыв