Если в трапецию вписана окружность, в задаче появляется несколько путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
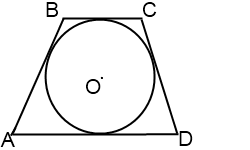
AB+CD=AD+BC
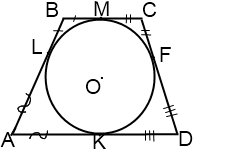
2. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что
AL=AK
BL=BM
CM=CF
DF=DK
3. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
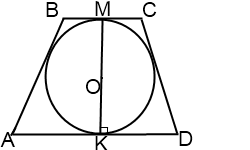
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
Рассмотрим базовую задачу.
Найти радиус вписанной в трапецию окружности, если точка касания делит боковую сторону на отрезки длиной m и n (CF=m, FD=n).
1) ∠ADC+∠BCD=180º (как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD);
2) так как точка O — точка пересечения биссектрис углов трапеции, то ∠ODF+∠OCF=1/2∙(∠ADC+∠BCD)=90º;
3) так как сумма углов треугольника равна 180º, то в треугольнике COD ∠COD=90º;
4) таким образом, треугольник COD прямоугольный, а OF — высота, проведенная к гипотенузе, CF и FD — проекции катета OC и OD на гипотенузу. Поскольку высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу,
![]()
Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как
![]()
А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков:
![]()
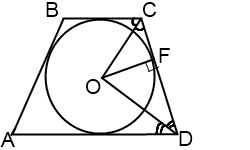
чему равен угол BCD?
Это зависит от данных условия.
Удвоенный OCF. А его можно найти через арктангенс, ведь мы уже знаем длины прилежащего и противолежащего катетов прямоугольного треугольника OCF. Ну или вычислить длину OC теоремой Пифагора и через арксинус вычислить угол.
BCD = 2arctan(OF/CF)