« »

Рубрика: Задачи по планиметрии

Как по сторонам треугольника найти медиану

Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.

Для начала рассмотрим задачу в общем виде.

Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.

 

AB=a, AC=b, BC=c.

найти медиану треугольника по его сторонам

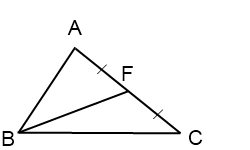
Решение.

На луче BF отложим отрезок FD, FD=BF.

найти длину медианы треугольника по его сторонам

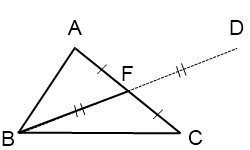
Соединим точку D с точками A и C.

нахождение медианы треугольника по его сторонам

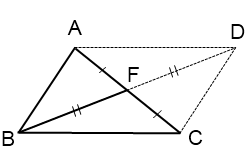
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.

Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),

BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,

    \[BD = \frac{1}{2}\sqrt {2({a^2} + {c^2}) - {b^2}} \]

Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:

    \[{m_b} = \frac{1}{2}\sqrt {2({a^2} + {c^2}) - {b^2}} \]

Переходим к рассмотрению конкретной задачи.

Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.

Решение:

Даны стороны треугольника. Найти медиану

 

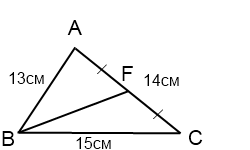
Применяя аналогичные рассуждения, получаем:

AC²+BD²=2(AB²+BC²).

Отсюда

14²+BD²=2(13²+15²)

BD²=2(169+225)-196=592

    \[BD = \sqrt {592} = \sqrt {16 \cdot 37} = 4\sqrt {37} (cm)\]

    \[BF = \frac{1}{2}DD = \frac{1}{2} \cdot 4\sqrt {37} = 2\sqrt {37} (cm)\]

Ответ:

    \[2\sqrt {37} cm\]

5 комментариев , 15 Янв 2013

5 комментариев на «Как по сторонам треугольника найти медиану»

  1. Ольга:
    19.11.2014 в 8:32 дп

    А пополам делить не надо?

    Ответить
  2. Аноним:
    22.12.2015 в 10:06 пп

    Спасибо большое

    Ответить
  3. Марат:
    31.01.2024 в 10:25 пп

    Здравствуйте! Нашел опечатку, как у вас написано: «Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.», меня из-за этого смутило умножение на 2, поэтому я поискал в интернете и оказывается нужно написать: «Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна УДВОЕННОЙ сумме квадратов его сторон.».

    Ответить
    • Светлана Иванова:
      03.02.2024 в 7:34 дп

      Марат, сторон в параллелограмме четыре, противоположные равны, поэтому сумму двух смежных сторон удваиваем. То есть сумма квадратов диагоналей параллелограмма равна сумме квадратов всех четырёх сторон. Либо удвоенной сумме двух смежных сторон.

      Ответить

Ваш отзыв