Узнать ещё

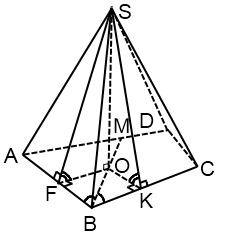
Если соседние двугранные углы при основании пирамиды равны, то вершина пирамиды проецируется на биссектрису угла между соответствующими соседними ребрами основания.

SO- высота пирамиды. Тогда точка O лежит на биссектрисе BM.

В частности,

1) Треугольная пирамида, в которой одна боковая грань перпендикулярна основанию, а две другие наклонены к основанию под равными углами.

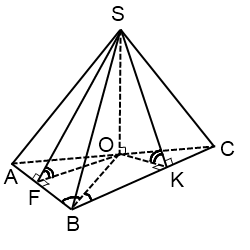Если в треугольной пирамиде одна из боковых граней перпендикулярна основанию, а две другие образуют с основанием равные углы, то высота пирамиды является высотой боковой грани, а ортогональная проекция вершины пирамиды — основание биссектрисы треугольника, лежащего в основании пирамиды.

Отсюда SO — высота пирамиды — лежит в боковой грани SAC, а BO — биссектриса треугольника ABC, то есть 

2) Пирамиды, в которых все двугранные углы при основании равны.