Рассмотрим примеры, в которых дан график функции, на котором отмечены точки. Нужно определить, в какой из этих точек значение производной наименьшее.
№1
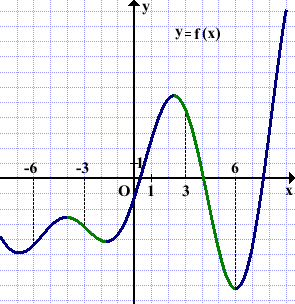
На рисунке изображён график функции y=f(x) и отмечены точки -6, -3, 3 и 6. В какой из этих точек значение производной наименьшее? В ответе указать эту точку.
 Решение:
Решение:
Точка x=6 — точка минимума функции y=f(x), поэтому производная в этой точке обращается в нуль: f'(6)=0.
Точка x=-6 принадлежит промежутку возрастания функции, поэтому производная в этой точке принимает положительное значение: f'(-6)>0.
Точки x=-3 и x=3 принадлежат промежуткам убывания функции, поэтому в этих точках значения производной отрицательны: f'(-3)<0 и f'(3)<0.
Остаётся сравнить f'(-3) и f'(3).
1 способ
Производная характеризует скорость изменения функции при изменении аргумента. На промежутке, которому принадлежит точка x=3, функция y=f(x) убывает быстрее, чем на промежутке, где лежит x=-3. Значит, по абсолютной величине больше значение производной в точке x=3: |f'(3)|>|f'(-3)|
А так как f'(-3)<0 и f'(3)<0, то f'(3)<f'(-3). Поэтому из данных точек наименьшее значение производная принимает в точке x=3.
2 способ
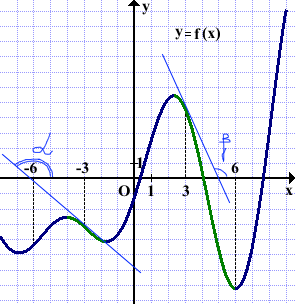 Значение производной в точке равно тангенсу угла, образуемого касательной к графику функции в этой точке и положительным направлением оси Ox.
Значение производной в точке равно тангенсу угла, образуемого касательной к графику функции в этой точке и положительным направлением оси Ox.
Проведем касательные к графику функции y=f(x) в точках x=-3 и x=3. Эти касательные образуют с положительным направлением оси абсцисс углы α и β.
Если α1>α2, то tg(α1)>tg(α2).
α>β, tg(α)>tg(β).
Следовательно, f'(-3)>f'(3).
Таким образом, значение производной наименьшее в точке x=3.
Ответ: 3.
№2
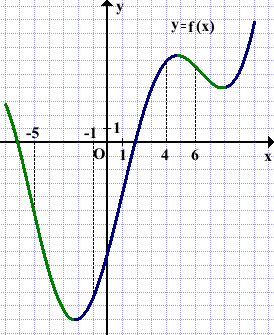
На рисунке изображён график функции y=f(x) и отмечены точки -5, -1, 4 и 6. В какой из этих точек значение производной наименьшее? В ответе указать эту точку.
 Решение:
Решение:
Точки x=-1 и x=4 принадлежат промежуткам возрастания функции y=f(x), поэтому производная f'(x) в этих точках принимает положительные значения: f'(-1)>) и f'(4)>0.
Точки x=-5 и x=6 принадлежат промежуткам убывания функции y=f(x), поэтому производная f'(x) в этих точках принимает отрицательные значения: f'(-5)<0 и f'(6)<0.
На промежутке, которому принадлежит точка x=-5, функция убывает быстрее, чем на промежутке, где лежит точка x=6. Поэтому |f'(-5)|>|f'(4)|.
Поскольку f'(-5)<0 и f'(6)<0, то f'(-5)<f'(6).
Таким образом, из четырёх данных точек наименьшее значение производная принимает в точке x=-5.
Ответ: -5.
Респект))