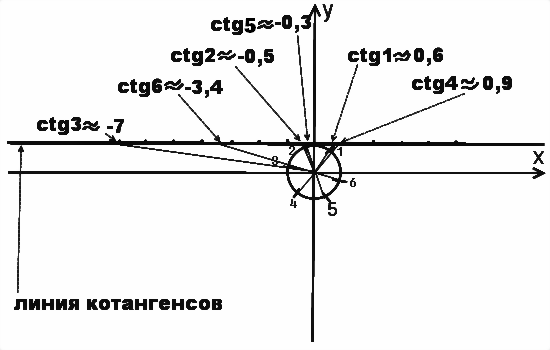
Единичная окружность и линия котангенсов позволяют оценить значения ctg 1, ctg 2, ctg 3, ctg 4, ctg 5 и ctg 6.
Сначала на единичной окружности находим и отмечаем углы в 1, 2, 3, 4, 5 и 6 радиан.
Теперь проведем линию котангенсов. Линия котангенсов — это прямая, касательная к единичной окружности в точке (0;1). То есть, линия котангенсов — это прямая y=1.
Проводим через начало координат и точку, соответствующую углу в 1 радиан, луч. Этот луч пересекает линию котангенсов в некоторой точке. Поскольку радиус единичной окружности равен единице, то отрезок, длина которого равна длине радиуса, на линии котангенсов соответствует 1. Получаем, что котангенс 1 приближенно равен 0,6. Аналогично, проводя лучи через другие отмеченные точки, получаем на линии котангенсов приближенные значения: котангенс 2 равен -0,5, котангенс 3 — -7, котангенс 4 — 0,9, котангенс 5 — -0,3, котангенс 6 — -3,4.
Разумеется, значения ctg 1, ctg 2, ctg 3, ctg 4, ctg 5 и ctg 6 можно найти с помощью калькулятора. Этот же способ оценки значений котангенса пригодится в тех случаях, когда калькулятор недоступен. При сравнении значений котангенса без калькулятора тоже вполне можно обойтись. Геометрическая интерпретация позволяет, например, сделать следующие выводы: ctg2 > ctg3, ctg1>ctg5.