Когда требуется найти тангенс 1, tg 2, tg 3, tg 4, tg 6, помогут единичная окружность и линия тангенсов.
Для начала отметим на единичной окружности углы в 1, 2, 3, 4, 5 и 6 радиан. Это можно сделать тремя способами.
1) 1 радиан — это приблизительно 57 градусов. Соответственно, через каждые 57 градусов отмечаем: 1 радиан, 2, 3…
2) 1 радиан — это угол, длина дуги которого равна радиусу окружности. В этом случае каждую следующую отметку ставим, откладывая приблизительно дугу длиной в радиус.
3) если вспомнить, что п — это приближенно 3,14, и рассчитать п/2, 3п/2, 2п, а 1,2, 3,4,5 и 6 радиан — ориентируясь на эти значения.
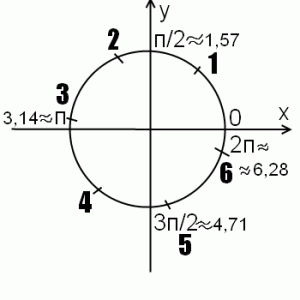
Получаем приблизительно такой чертеж:
Если нужно сравнить, например, tg1 и tg2, этого чертежа вполне достаточно. 1 радиан — угол 1й четверти, где тангенс положителен, а 2 радиана — угол 2й четверти, где тангенс отрицателен (см. как запомнить знаки тангенса). Поэтому tg1 > tg2.
Когда требуется сравнить тангенсы одного знака, например, tg 5 и tg 6, единичной окружности недостаточно. Найти значения tg1, tg2, tg3, tg4, tg6 можно также с помощью линии тангенсов.
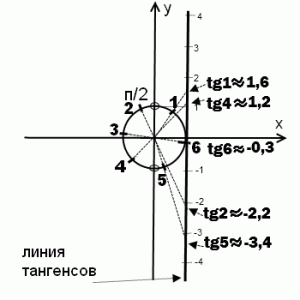
Линия тангенсов — это касательная к единичной окружности в точке (1;0). То есть линия тангенсов — это прямая x=1.
Если через точку О — начало отсчета- и отмеченный на единичной окружности угол в 1 радиан провести луч, то он пересечет линию тангенсов в точке, которая показывает значения tg 1. Поскольку окружность единичная, то значения 2,3,4 и т.д. получаем, откладывая на линии тангенсов длину радиуса. Соответственно, tg 1 получаем где-то посредине между 1 и 2, чуть ближе к 2. Аналогично на линии тангенсов определяем, чему равен тангенс 2, тангенс 3, тангенс 4, тангенс 5 и тангенс 6. Отсюда делаем вывод: tg5 < tg6, tg2>tg5, tg4<tg1.
Конечно, все эти значения можно получить с помощью калькулятора. Но в тех случаях, когда воспользоваться калькулятором нельзя, этот способ работает.
Получать значения тангенса и сравнивать их можно также с помощью графика функции y=tg x. Но это уже другая история.
Огромное спасибо! Все очень подробно и понятно!