Узнать ещё

Рассмотрим, что можно сказать о функции, анализируя график ее второй производной.

Что мы знаем связи второй производной

   

с исходной функцией y=f(x)?

1) Функция y=f(x) выпукла вниз на промежутках, где вторая производная положительна

   

2) Функция y=f(x) выпукла вверх на промежутках, где вторая производная отрицательна

   

3) Функция y=f(x) имеет критические точки второго рода в точках, в которых вторая производная равна нулю или не существует (речь идет только о внутренних точках области определения функции. Точки на концах области определения не рассматриваем).

4) Функция y=f(x) имеет точки перегиба в точках, в которых вторая производная  меняет знак.

5) С учетом того, что x0 — точка максимума функции f(x), если

   

точки максимума, если они есть, на графике второй производной лежат ниже оси OX.

Соответственно, x* — точка минимума функции f(x), если

   

поэтому точки минимума, если они есть, на графике второй производной лежат выше оси OX.

Пример.

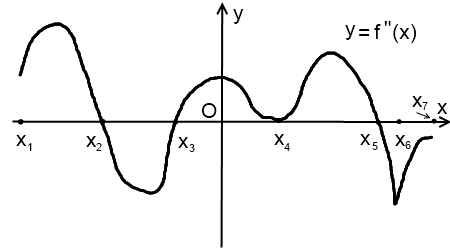
На промежутках (x1; x2) и (x3;x5) вторая производная неотрицательна (в точке x4 она равна нулю, но смены знака нет). Значит, на этих промежутках функция y=f(x) выпукла вниз.

На промежутках (x2; x3) и (x5; x7) вторая производная отрицательна. Поэтому на этих промежутках функция y=f(x) выпукла вверх.

В точках x2, x3, x4, x5 вторая производная равна нулю, в точке x6 — не существует. Это — критические точки второго рода.

Производная меняет знак в точках x2, x3, x5. Следовательно, это — точки перегиба.