Конус вписан в призму

« Призма вписана в конус Пирамида вписана в конус »

Конус вписан в призму

Конус вписан в призму, если его основание вписано в одно основание призмы, а вершина лежит в другом основании призмы. Соответственно, в этом случае призма описана около конуса.

конус вписан в призму

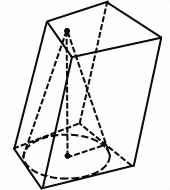
Вписать конус можно только в такую призму, в основание которой можно вписать окружность.

При решении задач на конус, вписанный в призму, удобно рассмотреть часть сечения комбинации тел плоскостью, проходящей через ось конуса и радиус вписанной в основание призмы окружности, проведенный в точку касания с одной из сторон. Для наклонной призмы это — прямоугольная трапеция, меньшая боковая сторона которой равна высоте конуса и призмы.

Чаще всего встречаются задачи на конус, вписанный в прямую призму. В этом случае ось конуса лежит на прямой, проходящей через центры вписанных в основание призмы окружностей.

призма описана около конуса

конус, вписанный в призму

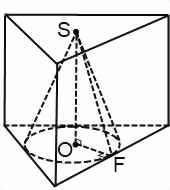
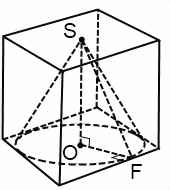
Если конус вписан в прямую призму, часть сечения комбинации тел плоскостью, проходящей через ось конуса, представляет собой прямоугольник. Решение задачи сводится к рассмотрению прямоугольного треугольника, катеты которого — высота конуса (и призмы) и радиус конуса (и вписанной в основание призмы окружности), а гипотенуза — образующая конуса.

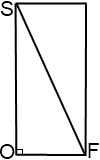сечение конуса в призме Здесь SO=H — высота конуса и высота призмы, OF=r — радиус конуса и радиус вписанной в основание призмы окружности, SF=l — образующая конуса. Найдем отношение объема конуса к объему описанной призмы.

$\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}\pi {r^2}H}}{{{S_{ocn}}H}} = \frac{{\pi {r^2}}}{{3{S_{ocn}}}} = \frac{{\pi {r^2}}}{{3pr}} = \frac{{\pi r}}{{3p}}.$

(Здесь p — полупериметр основания. Эта формула верна и для наклонной призмы).

В частности, отношение объема вписанного конуса к объему правильной треугольной призмы со стороной основания a

$\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi r}}{{3p}} = \frac{{\pi \cdot \frac{a}{{2\sqrt 3 }}}}{{3 \cdot \frac{{3a}}{2}}} = \frac{\pi }{{9\sqrt 3 }} = \frac{{\pi \sqrt 3 }}{{27}}.$

Для правильной четырехугольной призмы (то есть для прямоугольного параллелепипеда, основание которого — квадрат со стороной a) отношение объемов конуса и описанной призмы

$\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi r}}{{3p}} = \frac{{\pi \cdot \frac{a}{2}}}{{3 \cdot 2a}} = \frac{\pi }{{12}}.$