« »

Рубрика: Комбинации геометрических тел

Призма вписана в конус

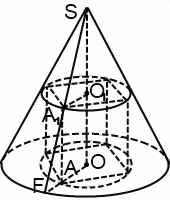
Призма вписана в конус, если одно из ее оснований лежит в основании конуса, а другое вписано в сечение конуса плоскостью, параллельной основанию. 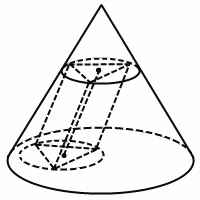наклонная призма в конусе

 

Можно сказать, что призма вписана в цилиндр, вписанный в конус.

 

 

 

 

 

конус описан около призмы

 

призма вписана в конус

 

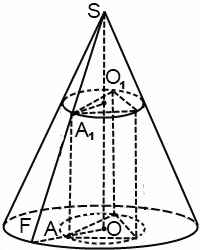
Если призма, вписанная в конус — прямая, то удобно рассмотреть  часть сечения комбинации тел плоскостью, проходящей через боковое ребро призмы и прямую, содержащую центры описанных около оснований призмы окружностей. Решение соответствующих задач  сводится к рассмотрению прямоугольного треугольника, катеты которого — радиус и высота конуса, а гипотенуза — образующая конуса.

сечение призмы в цилиндре

 

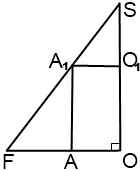
Например, в прямоугольном треугольнике SOF SO=H — высота конуса, FO=R — радиус конуса, SF=l — образующая конуса, AO=r — радиус окружности, описанной около основания призмы, AA1=h — боковое ребро и высота призмы.

 

Прямоугольные треугольники SFO и SA1O1 подобны (по общему острому углу S). Отсюда

    \[\frac{{SO}}{{S{O_1}}} = \frac{{FO}}{{{A_1}{O_1}}} = \frac{{SF}}{{S{A_1}}}, \Rightarrow \]

    \[\frac{H}{{H - h}} = \frac{R}{r} = \frac{l}{{\sqrt {{h^2} + {{(R - r)}^2}} }}.\]

 

 

 

 

 

Комментарии к записи Призма вписана в конус отключены , 23 Мар 2013

Обсуждение закрыто.