« »

Рубрика: Задачи по планиметрии

Как медиана делит треугольник

Медиана делит пополам не только сторону треугольника. Еще медиана делит треугольник на две равновеликие части. Рассмотрим, как применяется это свойство при решении задач.

Сначала разберемся, почему медиана делит треугольник на части, площади которых равны.

как медиана делит треугольник

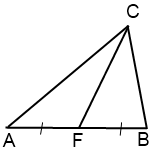
По формуле

    \[S = \frac{1}{2}ab\sin \alpha \]

    \[{S_{AFC}} = \frac{1}{2}AF \cdot FC \cdot \sin \angle AFC,\]

    \[{S_{BFC}} = \frac{1}{2}BF \cdot FC \cdot \sin \angle BFC.\]

Поскольку ∠AFC  и ∠BFC — смежные, то∠AFC +∠BFC=180º. А так как по формуле приведения  sin(180º — α)=sin α, то sin∠AFC=sin(180º -∠BFC) = sin∠BFC. Так как медиана CF делит сторону AB на две равные части: AF=FB, то имеем: 

    \[{S_{AFC}} = \frac{1}{2}AF \cdot FC \cdot \sin \angle AFC = \frac{1}{2}BF \cdot FC \cdot \sin \angle BFC = {S_{BFC}}\]

Переходим к рассмотрению задачи, для решения которой применим доказанное свойство.

На медиане BD треугольника ABC отметили точку M так, что BM:MD=3:1. Найти площадь треугольника ABC, если площадь треугольника AMD равна 3 см².

Точка делит медиану в отношении 3:1

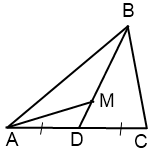
По доказанному, площади треугольников ABD и CBD равны. Выразим площадь треугольника ABС через площадь треугольника AMD:

    \[{S_{ABC}} = 2{S_{ABD}} = 2 \cdot \frac{1}{2}AD \cdot BD \cdot \sin \angle ADB = \]

    \[ = 2 \cdot \frac{1}{2}AD \cdot 4DM \cdot \sin \angle ADB = \]

    \[ = 8 \cdot \frac{1}{2}AD \cdot DM \cdot \sin \angle ADB = \]

    \[ = 8{S_{AMD}} = 8 \cdot 3 = 24c{m^2}.\]

 

1 отзыв , 23 Янв 2013

Один отзыв на «Как медиана делит треугольник»

  1. Дима:
    22.03.2019 в 12:36 пп

    Полезно свойство медианы! Применил для решения другой задачи

    Ответить

Ваш отзыв