sin arcctg

Найти sin (arcctg x)

Синус арккотангенса sin (arcctg x) удобно найти с помощью определений синуса, котангенса и арккотангенса и теоремы Пифагора.

По определению арккотангенса, если

$arcctgx = \alpha , \Rightarrow x = ctg\alpha$

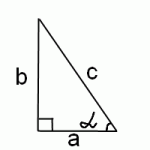
Поскольку котангенс в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему, то имеем:

$ctg\alpha = \frac{a}{b}.$

А нам нужен синус этого же угла альфа. Так как синус — это отношение противолежащего катета к гипотенузе, нам остается найти гипотенузу. По теореме Пифагора:

$c = \sqrt {{a^2} + {b^2}} .$

Отсюда имеем:

$\sin (arcctgx) = \frac{b}{{\sqrt {{a^2} + {b^2}} }},$

где

$x = \frac{a}{b}.$

Пример.

Найти sin (arcctg 5).

Арккотангенс 5 — это число альфа, котангенс которого равен 5. Котангенс в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему. Значит, в нашем случае прилежащий катет а=5, противолежащий b=1. Синус — это отношение противолежащего катета к гипотенузе. Осталось найти гипотенузу:

$c = \sqrt {{5^2} + {1^2}} = \sqrt {26.}$