« »

Рубрика: Легкое решение

cos (arctg x)

С помощью определения косинуса и тангенса в прямоугольном треугольнике, а также определения арктангенса и теоремы Пифагора найти косинус арктангенса  cos (arctg x) можно быстро, не  привлекая  дополнительные тригонометрические формулы.

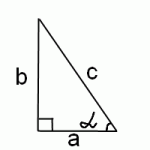   По определению арктангенса,  arctg x — это такое число альфа, что

    \[tg\alpha = x.\]

Тангенс угла альфа в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему:

    \[tg\alpha = \frac{b}{a}.\]

Нам нужно найти косинус этого же угла альфа. Поскольку косинус альфа равен отношению прилежащего катета к гипотенузе

    \[\cos \alpha = \frac{a}{c},\]

остается найти гипотенузу. По теореме Пифагора

    \[c = \sqrt {{a^2} + {b^2}} ,\]

а значит

    \[\cos (arctgx) = \frac{a}{{\sqrt {{a^2} + {b^2}} }},\]

где

    \[x = \frac{b}{a}.\]

Примеры.

1) Найти cos (artg (3/4)).

    \[arctg(3/4) = \alpha , \Rightarrow tg\alpha = \frac{3}{4}.\]

Поскольку тангенс альфа — это отношение противолежащего катета к прилежащему, то противолежащий катет b=3, прилежащий катет a=4. Нам нужно найти косинус этого же угла альфа. Так как косинус равен отношению прилежащего катета к гипотенузе, находим по теореме Пифагора гипотенузу

    \[c = \sqrt {{4^2} + {3^2}} = 5,\]

и получаем искомое значение:

    \[\cos (arcg(3/4)) = \frac{4}{5}.\]

2) Вычислить

    \[\cos (arctg\sqrt 2 ).\]

    \[a = 1,b = \sqrt {2,} \Rightarrow c = \sqrt {{1^2} + {{(\sqrt 2 )}^2}} = \sqrt {3,} \Rightarrow \]

    \[\cos (arctg\sqrt 2 ) = \frac{1}{{\sqrt 3 }}.\]

 

 

2 комментария , 10 Авг 2012

2 комментария на «cos (arctg x)»

  1. LKrus:
    07.09.2014 в 2:11 пп

    Спасибо, выручили. Материал изложен очень доступно.

    Ответить

Ваш отзыв