Легко найти синус арктангенса sin (arctg) с помощью определений тангенса и синуса в прямоугольном треугольнике, определения арктангенса и теоремы Пифагора.
Итак, найти sin (arctg x). Арктангенс икса — это такое число альфа,
![]()
что
![]()
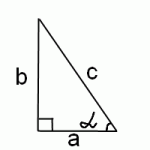
Но тангенс угла альфа в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
![]()
А синус этого угла — это отношение противолежащего катета к гипотенузе, то есть
![]()
Гипотенузу c найдем по теореме Пифагора:
![]()
Таким образом получили, что синус от арктангенса
![]()
где
![]()
1) Найти sin (arctg (3/4)).
Чтобы найти sin (arctg (3/4)), применим рассуждения для случая a=4, b=3. Отсюда
![]()
![]()
2) Найти sin(arctg 3)
a=1, b=3.
![]()
![]()
отчего же не продолжить?
Из tg α =x и tg α = b/a следует, что b=a*x. Подставим в sin(arctg())
= b/sqrt(a^2+b^2)=b/sqrt(a^2+a^2*x^2)=b/a*sqrt(1+x^2)=(b/a)/sqrt(1+x^2)=
=x/sqrt(1+x^2)
Это обычный путь, который предлагают в учебниках. Мне больше нравится геометрическая интерпретация :).