« »

Рубрика: Комбинации геометрических тел

Цилиндр вписан в призму

Призма описана около цилиндра, если ее основания — многоугольники, описанные около оснований цилиндра. Соответственно, цилиндр вписан в призму.

призма описанна около цилиндрацилиндр в призме

 

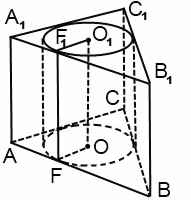
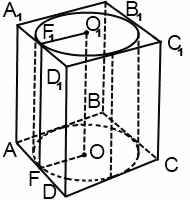
Цилиндр можно вписать в призму, если в основание призмы можно вписать окружность. Радиус вписанной окружности равен радиусу цилиндра. Высоты цилиндра и призмы равны. В школьном курсе изучается только прямой круговой цилиндр, соответственно, цилиндр в этом случае вписан в прямую призму.

Боковые грани описанной около цилиндра призмы являются касательными плоскостями к боковой поверхности цилиндра.

Найдем отношение объема призмы к объему вписанного в нее цилиндра:

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{S_{ocn}} \cdot H}}{{\pi {r^2}H}} = \frac{{prH}}{{\pi {r^2}H}} = \frac{p}{{\pi r}}.\]

  p — полупериметр основания призмы, r — радиус вписанной в основание призмы окружности и радиус цилиндра, H — высота призмы и высота цилиндра.

В частности, отношение объема правильной треугольной призмы к объему вписанного цилиндра

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{p}{{\pi r}} = \frac{{\frac{{3a}}{2}}}{{\pi \cdot \frac{a}{{2\sqrt 3 }}}} = \frac{{3\sqrt 3 }}{\pi }.\]

Отношение объема правильной четырехугольной призмы к объему вписанного цилиндра

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{p}{{\pi r}} = \frac{{2a}}{{\pi \cdot \frac{a}{2}}} = \frac{4}{\pi }.\]

Для правильной шестиугольной призмы это отношение равно

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{p}{{\pi r}} = \frac{{3a}}{{\pi \cdot \frac{{a\sqrt 3 }}{2}}} = \frac{6}{{\pi \sqrt 3 }} = \frac{{2\sqrt 3 }}{\pi }.\]

Отношение площади боковой поверхности призмы к боковой поверхности вписанного цилиндра:

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}} \cdot H}}{{2\pi rH}} = \frac{{{P_{ocn}}}}{{2\pi r}}.\]

Поскольку половина периметра основания — полупериметр, 

    \[\frac{{{P_{ocn}}}}{2} = p, \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{p}{{\pi r}}.\]

Таким образом, если цилиндр вписан в призму, отношение площади боковой поверхности призмы к боковой поверхности цилиндра равно отношению объема призмы к объему вписанного цилиндра. В частности, отношение площади боковой поверхности правильной треугольной призмы к площади боковой поверхности вписанного цилиндра

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}}}}{{2\pi r}} = \frac{{3a}}{{2\pi \cdot \frac{a}{{2\sqrt 3 }}}} = \frac{{3\sqrt 3 }}{\pi }.\]

Отношение боковой поверхности правильной четырехугольной призмы к боковой поверхности вписанного цилиндра

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}}}}{{2\pi r}} = \frac{{4a}}{{2\pi \cdot \frac{a}{2}}} = \frac{4}{\pi }.\]

Отношение боковой поверхности правильной шестиугольной призмы к боковой поверхности вписанного цилиндра

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}}}}{{2\pi r}} = \frac{{6a}}{{2\pi \cdot \frac{{a\sqrt 3 }}{2}}} = \frac{6}{{\pi \sqrt 3 }} = \frac{{2\sqrt 3 }}{\pi }.\]

При решении задач, в которых цилиндр вписан в призму, можно рассматривать часть сечения комбинации тел плоскостью, проходящей через ось цилиндра. Для прямой призмы это сечение — прямоугольник, стороны которого равны радиусу цилиндра и высоте цилиндра. Например, AA1O1O: AA1=H, AO=r.

 

Ваш отзыв , 18 Мар 2013

Ваш отзыв