« »

Рубрика: Задачи по планиметрии

В ромб вписана окружность

Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.

окружность в ромбе Точка касания вписанной в ромб окружности делит его сторону на отрезки

В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.

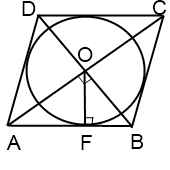
Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).

    \[AO = \frac{1}{2}AC = \frac{1}{2}{d_1};BO = \frac{1}{2}BD = \frac{1}{2}{d_2}\]

    \[OF \bot AB\]

— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда

    \[OF = \sqrt {AO \cdot OB} , \Rightarrow r = \sqrt {mn} \]

    \[AO = \sqrt {AF \cdot AB} , \Rightarrow \frac{1}{2}{d_1} = \sqrt {m \cdot (m + n)} \]

    \[OB = \sqrt {FB \cdot AB} , \Rightarrow \frac{1}{2}{d_2} = \sqrt {n \cdot (m + n)} .\]

Высота ромба через радиус вписанной окружности

    \[h = 2r\]

Радиус вписанной в ромб окружности

Радиус вписанной окружности можно найти по формуле

    \[r = \frac{S}{p}\]

S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).

Соответственно, площадь ромба через радиус вписанной в него окружности

    \[S = pr\]

Поскольку площадь ромба также равна

    \[S = \frac{1}{2}{d_1}{d_2},\]

    \[ \Rightarrow \frac{1}{2}{d_1}{d_2} = pr\]

    \[ \Rightarrow r = \frac{{\frac{1}{2}{d_1}{d_2}}}{p} = \frac{{{d_1}{d_2}}}{{2p}} = \frac{{{d_1}{d_2}}}{{4a}},\]

Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как

    \[S = pr = 2(m + n)\sqrt {mn} .\]

 

 

Ваш отзыв , 14 Апр 2013

Ваш отзыв