« »

Рубрика: Комбинации геометрических тел

Конус вписан в пирамиду

 

 

Конус вписан в пирамиду, если его основание вписано в основание пирамиды, а вершина совпадает с вершиной пирамиды. Соответственно, в этом случае пирамида описана около конуса.

конус в пирамиде                      конус, вписанный в пирамиду

 

 

 

 

 

 

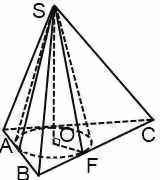
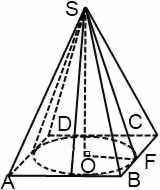
Конус может быть вписан в пирамиду, если основание пирамиды — многоугольник, в который можно вписать окружность, а вершина пирамиды проецируется в центр этой окружности. Другой вариант: конус можно вписать в пирамиду, если высоты ее боковых граней равны между собой. Отсюда, в частности, следует, что в любую правильную пирамиду можно вписать конус.

Каждая из плоскостей, содержащих боковую грань описанной пирамиды, является касательной к конусу плоскостью (то есть плоскостью, проходящей через образующую  конуса перпендикулярно осевому сечению конуса, проведенному через эту образующую). Высоты боковых граней пирамиды есть образующие конуса. Высота вписанного конуса совпадает с высотой пирамиды. Радиус конуса равен радиусу вписанной в основание пирамиды окружности.

Найдем отношение объема вписанного конуса к объему пирамиды:

    \[\frac{{{V_k}}}{{{V_n}}} = \frac{{\frac{1}{3}\pi {r^2}H}}{{\frac{1}{3}{S_{ocn}}H}} = \frac{{\pi {r^2}}}{{{S_{ocn}}}}.\]

В частности, отношение объема вписанного конуса к объему правильной пирамиды для правильной треугольной пирамиды равно

    \[\frac{{{V_k}}}{{{V_n}}} = \frac{{\pi {{(\frac{a}{{2\sqrt 3 }})}^2}}}{{\frac{{{a^2}\sqrt 3 }}{4}}} = \frac{{4\pi {a^2}}}{{12\sqrt 3 {a^2}}} = \frac{\pi }{{3\sqrt 3 }},\]

для правильной четырехугольной пирамиды —

    \[\frac{{{V_k}}}{{{V_n}}} = \frac{{\pi {{(\frac{a}{2})}^2}}}{{{a^2}}} = \frac{\pi }{4},\]

для правильной шестиугольной пирамиды —

    \[\frac{{{V_k}}}{{{V_n}}} = \frac{{\pi {{(\frac{{a\sqrt 3 }}{2})}^2}}}{{\frac{{3{a^2}\sqrt 3 }}{2}}} = \frac{\pi }{{2\sqrt 3 }}.\]

(Формулу площади правильного треугольника и формулу площади правильного шестиугольника легко запомнить с помощью ассоциаций).

 Теперь найдем отношение площади боковой поверхности вписанного конуса к боковой поверхности правильной пирамиды. Так как апофема  пирамиды m равна образующей конуса l, имеем:

    \[\frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = \frac{{\pi rl}}{{pm}} = \frac{{\pi r}}{p}.\]

В частности, отношение боковой поверхности вписанного конуса к боковой поверхности правильной треугольной пирамиды

    \[\frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = \frac{{\pi \cdot \frac{a}{{2\sqrt 3 }}}}{{\frac{{3a}}{2}}} = \frac{\pi }{{3\sqrt 3 }},\]

для правильной четырехугольной пирамиды —

    \[\frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = \frac{{\pi \cdot \frac{a}{2}}}{{2a}} = \frac{\pi }{4},\]

для правильной шестиугольной пирамиды —

    \[\frac{{{S_{bok.k}}}}{{{S_{bok.p}}}} = \frac{{\pi \cdot \frac{{a\sqrt 3 }}{2}}}{{3a}} = \frac{\pi }{{2\sqrt 3 }}.\]

 

 

 

 

 

Ваш отзыв , 16 Апр 2013

Ваш отзыв