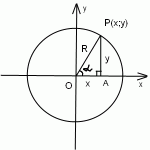
Чтобы ввести определения синуса, косинуса, тангенса и котангенса для произвольного угла, воспользуемся тригонометрической окружностью.
Рассмотрим прямоугольный треугольник AOP. По определению тригонометрических функций острого угла, имеем:
![\[\sin \alpha = \frac{{AP}}{{OP}},\cos \alpha = \frac{{OA}}{{OP}},tg\alpha = \frac{{AP}}{{OA}},ctg\alpha = \frac{{OA}}{{AP}}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-84724eda245f075d0a113f7f6f202b87_l3.png "Rendered by QuickLaTeX.com")
Но OA=x, AP=y, OP=R. Отсюда,
![\[\sin \alpha = \frac{y}{R},\cos \alpha = \frac{x}{R},tg\alpha = \frac{y}{x},ctg\alpha = \frac{x}{y}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f2008dc96b9c253d7b3add77558e0b21_l3.png "Rendered by QuickLaTeX.com")
Изменение радиуса окружности не влияет на значения синуса и косинуса. Поэтому удобно выбрать R=1. Такую окружность называют единичной. Таким образом,
![\[\sin \alpha = y,\cos \alpha = x\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f2dda03fe348294529b1fd5672302871_l3.png "Rendered by QuickLaTeX.com")
Итак, чем синус отличается от косинуса? Легко запомнить синус и косинус с помощью ассоциации. Косинус — колобок (и начинаются оба слова с ко-). Колобку как удобнее двигаться: прыгать вверх-вниз или катиться влево-вправо? Правильно, с его фигурой ему легче передвигаться по горизонтали, то есть по оси OX.
Ассоциация: косинус — колобок — x. Ну а синус, соответственно — y.Таким образом, синус произвольного угла — это ордината y точки P на единичной окружности, полученной из точки A поворотом вокруг начала координат на угол альфа, косинус произвольного угла — ее абсцисса x.
Эта ассоциация поможет нам легко определять знаки синуса и косинуса, а также находить частные случаи решения простейших тригонометрических уравнений.