Рассмотрим базовые задачи на подобные треугольники в трапеции.
I. Точка пересечения диагоналей трапеции — вершина подобных треугольников.

Рассмотрим треугольники AOD и COB.
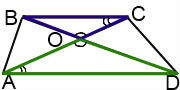
Визуализация облегчает решение задач на подобие. Поэтому подобные треугольники в трапеции выделим разными цветами.
1) ∠AOD=∠COB (как вертикальные);
2)∠DAO=∠BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
Следовательно, треугольники AOD и COB подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
![]()
Задача.
Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.
Решение:
AO=9 см, CO=5 см, BD=28 см. BO =?, DO- ?
Доказываем подобие треугольников AOD и COB. Отсюда
![]()
Выбираем нужные отношения:
![]()
Пусть BO=x см, тогда DO=28-x см. Следовательно,
![]()
![]()
![]()
![]()
BO=10 см, DO=28-10=18 см.
Ответ: 10 см, 18 см.
Задача
Известно, что О — точка пересечения диагоналей трапеции ABCD (AD ∥ BC). Найти длину отрезка BO, если AO:OC=7:6 и BD=39 см.
Решение:
Аналогичн0, доказываем подобие треугольников AOD и COB и
![]()
Пусть BO=x см, тогда DO=39-x см. Таким образом,
![]()
![]()
![]()
Ответ: 18 см.
II. Продолжения боковых сторон трапеции пересекаются в точке.
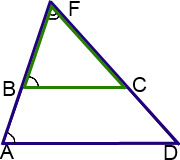
Аналогично задаче I, рассмотрим треугольники AFD и BFC:
1) ∠F — общий;
2)∠ DAF=∠CBF (как соответственные углы при BC ∥ AD и секущей AF).
Следовательно, треугольники AFD и BFC подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
![]()
Задача
Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке F. Меньшее основание BC равно 4 см, BF=5 см, AB=15 см. Найти большее основание трапеции.
Решение:
Доказываем, треугольники AFD и BFC — подобны.
Следовательно,
![]()
![]()
![]()
![]()
![]()
Ответ: 16 см.
В следующий раз рассмотрим задачи на отношение площадей подобных треугольников.
Большое спасибо вам,все рассказано очень доходчиво