Чтобы понять, как решать задачи с трапецией, полезно запомнить три основных пути решения.
I. Провести две высоты. 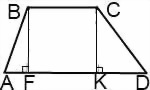
Ia. Четырехугольник BCKF — прямоугольник (так как у него все углы прямые). Следовательно, FK=BC.
AD=AF+FK+KD, отсюда AD=AF+BC+KD.
Треугольники ABF и DCK — прямоугольные.
(Следует учесть и другой вариант:
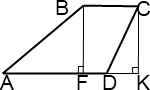 Ib.
Ib.
В этом случае AD=AF+FD=AF+FK-DK=AF+BC-DK.)
Ic. Если трапеция равнобедренная, решение задачи упрощается:
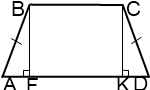 В этом случае прямоугольные треугольники ABF и DCK равны, например, по катету и гипотенузе (AB=CD по условию, BF=CK как высоты трапеции). Из равенства треугольников следует равенство соответствующих сторон:
В этом случае прямоугольные треугольники ABF и DCK равны, например, по катету и гипотенузе (AB=CD по условию, BF=CK как высоты трапеции). Из равенства треугольников следует равенство соответствующих сторон:
AF=KD=(AD-FK):2=(AD-BC):2.
II. Провести прямую, параллельную боковой стороне.
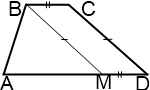 IIa. BM∥CD. Так как BC∥AD (как основания трапеции), то BCDM — параллелограмм. Следовательно, MD=BC, BM=CD, AM=AD-BC.
IIa. BM∥CD. Так как BC∥AD (как основания трапеции), то BCDM — параллелограмм. Следовательно, MD=BC, BM=CD, AM=AD-BC.
IIb. В частности, для равнобедренной трапеции
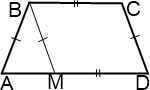 BM∥CD. Так как CD=AB, то и BM=AB. То есть получаем равнобедренный треугольник ABM и параллелограмм BCDM.
BM∥CD. Так как CD=AB, то и BM=AB. То есть получаем равнобедренный треугольник ABM и параллелограмм BCDM.
III. Продолжить боковые стороны и получить треугольник.
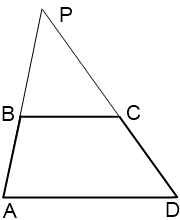 Прямые AB и CD пересекаются в точке P.
Прямые AB и CD пересекаются в точке P.
Треугольники APD и BPC подобны по двум углам (угол P — общий, ∠PAD= ∠PBC как соответственные при BC∥AD и секущей AP).
Следовательно, их стороны пропорциональны:
![]()
Эти три подхода к решению задач на трапецию — основные. Помимо них, существует много других способов. Некоторые рассмотрены на этом сайте. Например, здесь — как решать задачи с трапецией, у которой диагонали перпендикулярны.
СПАСИБО,прошу напишите материал о сечениях куба,проходящих через середину ребер.Заранее спасибо!
Постараюсь. Но быстро не обещаю — времени не хватает.