Узнать ещё

Рассмотрим  задачи, в которых биссектриса угла трапеции делит противоположное основание на отрезки.

Мы уже имели дело с похожей задачей на биссектрису угла параллелограмма, а также рассматривали частный случай для трапеции (когда основание трапеции равно ее боковой стороне, биссектриса трапеции совпадает с ее диагональю).

I. Биссектриса острого угла при большем основании трапеции делит другое основание на отрезки.

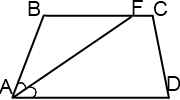 1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).

2) ∠DAF=∠BFA (как внутренние накрест лежащие при     AD∥BC и секущей AF).

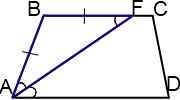 3) Следовательно, ∠BAF=∠BFA.

4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку равнобедренного треугольника).

5) Следовательно, AB=BF.

 II. Биссектриса тупого угла при меньшем основании трапеции делит другое основание на отрезки.

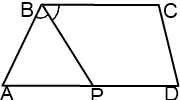 Аналогично доказывается, что треугольник ABP — равнобедренный:

1) ∠ABP=∠CBP (так как BP — биссектриса ∠ABC по условию).

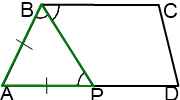2) ∠CBP=∠APB (как внутренние накрест лежащие при AD∥BC и секущей BP).

3) Следовательно, ∠ABP=∠APB.

4) Следовательно, треугольник ABP — равнобедренный с основанием BP (по признаку равнобедренного треугольника).

5) Следовательно, AB=AP.

Вывод: в этом случае

биссектриса угла трапеции отсекает от нее равнобедренный треугольник.

Эта задачи — базовые. На их основе существует много других задач.

В следующий раз рассмотрим задачи на пересечение двух биссектрис трапеции.