« »

Рубрика: Легкое решение

cos (arcctg x)

Косинус арккотангенса cos (arcctg x) легко найти через определения косинуса, котангенса, арккотангенса и теорему Пифагора. Геометрическая интерпретация  упрощает понимание примеров такого рода.

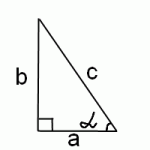Итак, нужно найти cos (arcctg x). По определению, arcctg  x — это такое число альфа, котангенс которого равен x.

    \[arcctgx = \alpha , \Rightarrow ctg\alpha = x.\]

Поскольку в прямоугольном треугольнике котангенс — это отношение прилежащего катета к противолежащему, то

    \[ctg\alpha = \frac{a}{b}.\]

А нам нужен косинус этого же угла альфа. Косинус равен отношению прилежащего катета к гипотенузе:

    \[\cos \alpha = \frac{a}{c}.\]

Таким образом, остается найти гипотенузу c. Это делаем по теореме Пифагора:

    \[c = \sqrt {{a^2} + {b^2}} ,\]

и окончательно имеем:

    \[\cos (arcctgx) = \frac{a}{{\sqrt {{a^2} + {b^2}} }},\]

где

    \[x = \frac{a}{b}.\]

Примеры.

1)Найти cos (arcctg (5/12)).

    \[arcctg\frac{5}{{12}} = \alpha , \Rightarrow ctg\alpha = \frac{5}{{12}}\]

А так как котангенс — это отношение прилежащего катета к противолежащему, то прилежащий катет a=5, противолежащий катет b=12. Нам надо найти косинус этого же угла альфа. Поскольку косинус равен отношению прилежащего катета к гипотенузе, ищем гипотенузу. По теореме Пифагора:

    \[c = \sqrt {{5^2} + {{12}^2}} = 13,\]

отсюда

    \[\cos (arcctg\frac{5}{{12}}) = \frac{5}{{13}}.\]

2) Найти cos (arcctg √2).

Здесь x=√2, значит a=√2, b=1. Отсюда

    \[c = \sqrt {{{(\sqrt 2 )}^2} + {1^2}} = \sqrt 3 , \Rightarrow \cos (arcctg\sqrt 2 ) = \sqrt {\frac{2}{3}} = \frac{{\sqrt 6 }}{3}.\]

 

 

1 отзыв , 12 Авг 2012

Один отзыв на «cos (arcctg x)»

  1. миша:
    09.06.2014 в 12:30 пп

    Спасибо,разобрался)))

    Ответить

Ваш отзыв