« »

Рубрика: Легкое решение

cos (arcsin x)

Косинус арксинуса cos (arcsin x) легко вычисляется на основании определения синуса, косинуса, арксинуса и теоремы Пифагора.

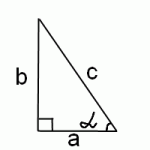По определению арксинуса: если  arcsin x = α, то sin α = x.

В прямоугольном треугольнике sin α равен отношению противолежащего катета к гипотенузе:

    \[\sin \alpha = \frac{b}{c}.\]

Нам нужно вычислить косинус этого же угла α. По определению, косинус — это отношение прилежащего катета к гипотенузе. В нашем случае:

    \[\cos \alpha = \frac{a}{c}.\]

Таким образом, остается найти прилежащий катет по теореме Пифагора: 

    \[a = \sqrt {{c^2} - {b^2}} .\]

Отсюда получаем искомый косинус арксинуса х:

    \[\cos (\arcsin x) = \frac{{\sqrt {{c^2} - {b^2}} }}{c},\]

где 

    \[x = \frac{b}{c}.\]

Хотя найти cos (arcsin x) можно и другим способом, с применением тригонометрической единицы, геометрическая интерпретация — инструмент, позволяющий в примерах такого вида обойтись без использования многих тригонометрических формул.

Примеры:

1) Найти cos (arcsin (5/13)).

Арксинус 5/13 — это число, синус которого равен 5/13. Синус — отношение противолежащего катета к гипотенузе, следовательно противолежащий катет b = 5, гипотенуза c = 13. По теореме Пифагора находим прилежащий катет

    \[a = \sqrt {{{13}^2} - {5^2}} = 12.\]

Отсюда

    \[\cos (\arcsin \frac{5}{{13}}) = \frac{{12}}{{13}}.\]

2) Вычислить cos (arcsin (1/3)).

В этом примере x=1/3, отсюда противолежащий катет b=1, гипотенуза c=3. Находим прилежащий катет a:

    \[a = \sqrt {{3^2} - {1^2}} = \sqrt 8 = 2\sqrt 2 .\]

Отсюда искомое значение  cos (arcsin (1/3)) 

    \[\cos (\arcsin \frac{1}{3}) = \frac{{2\sqrt 2 }}{3}.\]

3) Вычислить cos (arcsin (-1/3)).

так как arcsin (-α)= -arcsin α, а cos (- α)= cos α, то cos (arcsin (-1/3)) = cos (- arcsin (1/3)) =

    \[ = \cos (\arcsin \frac{1}{3}) = \frac{{2\sqrt 2 }}{3}.\]

4 комментария , 11 Авг 2012

4 комментария на «cos (arcsin x)»

  1. миша:
    09.06.2014 в 12:19 пп

    отличная статья! Помогла разобраться)

    Ответить
  2. алиса:
    03.12.2015 в 3:35 дп

    Спасибо, доступно и без всяких ненужностей

    Ответить
  3. Руслан:
    18.07.2019 в 1:28 пп

    cos(arcsin x)=(1-x^2)^0.5
    Не судьба сразу принять с=1, b=x, тогда cos(arcsin x)=(1-x^2)^0.5?
    Тогда не нужно никаких обыкновенных дробей и программистам мозг не ломать.

    Ответить
    • Светлана Иванова:
      28.08.2019 в 9:24 пп

      Руслан, так готовая формула в школьном курсе есть. А это — ещё один способ, геометрически.

      Ответить

Ваш отзыв