tg (arcsin x)

« cos (arcctg x) Найти тангенс арккосинуса »

tg (arcsin x)

Тангенс арксинуса tg (arcsin x) легко найти, используя определения тангенса, синуса, арксинуса и теорему Пифагора. Дополнительно привлекать тригонометрические формулы при таком решении не требуется.

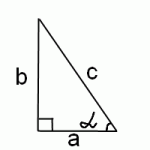Итак, надо найти tg (arcsin x). По определению арксинуса, arcsin x — это такое число α, синус которого равен x:

$\arcsin x = \alpha , \Rightarrow \sin \alpha = x.$

Но в прямоугольном треугольнике sin α равен отношению противолежащего катета к гипотенузе:

$\sin \alpha = \frac{b}{c},$

а нам нужно найти тангенс этого же угла. По определению, тангенс — это отношение противолежащего катета к прилежащему:

$tg\alpha = \frac{b}{a}.$

Таким образом, нам осталось найти прилежащий катет a. Сделаем это по теореме Пифагора:

$a = \sqrt {{c^2} - {b^2}} .$

Отсюда находим tg (arcsin x):

$tg(\arcsin x) = \frac{b}{{\sqrt {{c^2} - {b^2}} }},$

где

$x = \frac{b}{c}.$

Примеры.

1) Найти tg (arcsin 3/5).

Арксинус 3/5 — это такое число α, синус которого равен 3/5. Но синус α — это отношение противолежащего катета к гипотенузе. Значит, в нашем случае противолежащий катет b = 3, гипотенуза c = 5. Тангенс этого угла α — это отношение противолежащего катета к прилежащему. Прилежащий катет находим по теореме Пифагора:

$a = \sqrt {{5^2} - {3^2}} = 4.$