Рассмотрим решения неравенств вида ctgx>a и ctgx<a на единичной окружности.
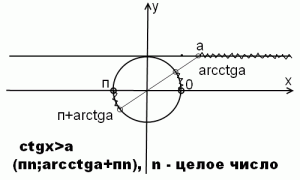
1) ctg x>a (здесь и далее а — положительное число).
Решать неравенства с котангенсом можно как с помощью графика функции y=ctg x, так и с использованием единичной окружности. Единичная окружность особенно полезна в тех случаях, когда требуется решить систему из нескольких неравенств. Именно поэтому мы будем рассматривать решение неравенства ctg x больше a не на периоде (0; п), а на всей единичной окружности (исключая точки вида пn, где n- целое число, которые не входят в область определения котангенса. Эти точки никогда не включаются в ответ, даже если неравенство нестрогое).
Строим единичную окружность и проводим линию котангенсов. Поскольку радиус окружности равен 1, единичный отрезок равен длине радиуса. Проводим прямую через начало отсчета — точку О — и точку a. Эта прямая пересекает единичную окружность в двух точках: arcctg a и arcctg a+п. На линии котангенсов значениям ctg x>a соответствуют все точки, расположенные справа от точки a. Заштриховываем эту часть линии котангенсов и соответствующий ей интервал единичной окружности.
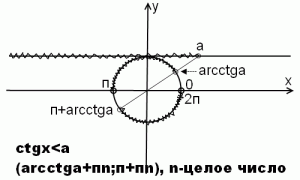
2) ctgx<a
Решениям неравенства ctgx<a на линии котангенсов соответствует часть, расположенная левее точки a. Соответствующая дуга на единичной окружности — (arcctg a; п). Чтобы учесть все промежутки, на которых ctg x меньше a, к каждому концу интервала прибавляем пn, где n — целое число.
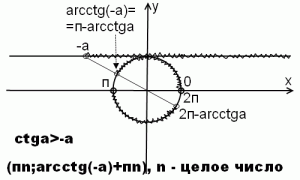
3) ctgx>-a
Котангенс больше -a правее точки -a на линии котангенсов. Соответствующий интервал на окружности — (0;arcctg(-a)), после упрощения — (0; п-arcctg a). К каждому из концов промежутка прибавляем пn, где n — целое число: (пn;п-arcctga+пn).
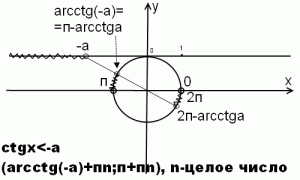
4) ctgx<-a
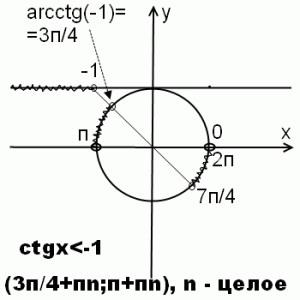
Пример.
Решить неравенство ctg x<-1.