Узнать ещё

Как запомнить  формулы приведения тригонометрических функций? Это легко, если использовать ассоциацию.Данная ассоциация придумана не мной. Как уже говорилось, хорошая ассоциация должна «цеплять», то есть вызывать яркие эмоции. Не могу назвать эмоции, вызываемые этой ассоциацией, позитивными. Но она дает результат — позволяет запоминать формулы приведения, а значит, имеет право на существование. В конце концов, если она вам не понравится, вы же ее можете не использовать, правильно?

Формулы приведения имеют вид: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запоминаем, что +α дает движение против часовой стрелки, — α  — движение по часовой стрелке.

Для работы с формулами приведения нужны два пункта:

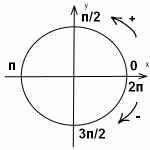1) ставим знак, который имеет начальная функция (в учебниках пишут: приводимая. Но, чтобы не запутаться, лучше назвать ее начальной), если считать α углом I четверти, то есть маленьким.

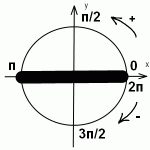
2) Горизонтальный диаметр — π±α, 2π±α, 3π±α… — в общем, когда нет дроби — название функции не меняет. Вертикальный π/2±α, 3π/2±α, 5π/2±α…- когда дробь есть — название функции меняет: синус — на косинус, косинус — на синус, тангенс — на котангенс и котангенс — на тангенс.

Теперь, собственно, ассоциация:

вертикальный диаметр (есть дробь) —

пьяный стоит. Что с ним случится рано

или поздно? Правильно, упадет.

Название функции изменится.

Если же диаметр горизонтальный — пьяный уже лежит. Спит, наверное. С ним уже ничего  не случится, он уже принял горизонтальное положение. Соответственно, название функции не меняется.

То есть sin(π/2±α), sin(3π/2±α), sin(5π/2±α) и т.д. дают ±cosα,

а sin(π±α), sin(2π±α), sin(3π±α), … —  ±sinα.

Как запомнить знаки тригонометрических функций по четвертям, уже знаем.

Как это работает? Смотрим на примерах.

1) cos(π/2+α)=?

Становимся на π/2. Поскольку +α — значит, идем вперед, против часовой стрелки. Попадаем во II четверть, где косинус имеет знак «-«. Название функции меняется («пьяный стоит», значит — упадет). Итак,

cos(π/2+α)=-sin α.

2) tg(2π-α)=?

Становимся на 2π. Так как -α — идем назад, то есть по часовой стрелке. Попадаем в IV четверть, где тангенс имеет знак «-«. Название функции не меняется (диаметр горизонтальный, «пьяный  уже лежит»). Таким образом, tg(2π-α)=- tgα.

3) ctg²(3π/2-α)=?

Примеры, в которых функция возводится в четную степень, решаются еще проще. Четная степень «-» убирает, то есть надо только выяснить, меняется название функции или остается. Диаметр вертикальный (есть дробь, «пьяный стоит», упадет), название функции меняется. Получаем: ctg²(3π/2-α)= tg²α.