« »

Рубрика: Легкое решение

Найти котангенс арккосинуса

Найти котангенс арккосинуса ctg (arccos x) на основании определений косинуса, котангенса, арккосинуса и теоремы Пифагора очень легко. На чертеже прямоугольного треугольника этот способ решения демонстрируется наглядно.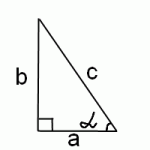Арккосинус икс — это такое число альфа, косинус которого равен x:

    \[\arccos x = \alpha , \Rightarrow \cos \alpha = x.\]

Поскольку косинус в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе, то в нашем случае

    \[\cos \alpha = \frac{a}{c}.\]

А нам нужен котангенс этого же угла альфа. Поскольку котангенс — это отношение прилежащего катета к противолежащему:

    \[ctg\alpha = \frac{a}{b},\]

нам остается найти противолежаший катет b. По теореме Пифагора:

    \[b = \sqrt {{c^2} - {a^2}} , \Rightarrow ctg(\arccos x) = \frac{a}{{\sqrt {{c^2} - {a^2}} }},\]

где

    \[x = \frac{a}{c}.\]

Примеры.

1) Найти ctg (arccos (1/3)).

Арккосинус 1/3 равен числу α, значит cosα=1/3. А так как косинус — это отношение прилежащего катета к гипотенузе, то прилежащий катет a=1, гипотенуза c=3. Котангенс α равен отношению прилежащего катета к противолежащему. Противолежащий катет b находим по теореме Пифагора:

    \[b = \sqrt {{3^2} - {1^2}} = \sqrt 8 = 2\sqrt 2 , \Rightarrow ctg(\arccos \frac{1}{3}) = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}.\]

2) Найти ctg (arccos (4/5)).

arccos (4/5)=α, значит cosα=4/5. Косинус равен отношению прилежащего катета к гипотенузе, отсюда a=4, c=5. По теореме Пифагора, b=3. Котангенс — это отношение прилежащего катета к противолежащему, значит ctg (arccos (4/5))=4/3.

Ваш отзыв , 19 Авг 2012

Ваш отзыв