Узнать ещё

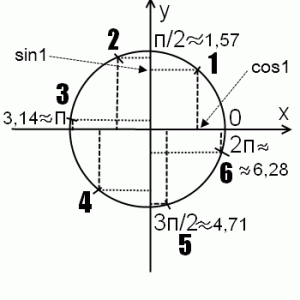
Легко сравнить cos 1 и tg 1, cos 2 и tg 2, sin 1 и tg 1, sin 2 и tg 2, cos 2 и ctg 2 и т.д. с помощью единичной окружности.

Для этого достаточно помнить, что косинус — это абсцисса точки на единичной окружности, а синус — ее ордината, и уметь находить радианы на окружности.

Легче всего сравнить sin 2 и tg 2, sin 2 и ctg 2, sin 3 и tg 3, sin 4 и tg 4, cos 6 и tg 6 и другие подобные примеры, в которых сравниваемые величины имеют разные знаки.

2 радиана — угол второй четверти, где синус положителен, а тангенс — отрицателен. Поскольку любое положительное число больше любого отрицательного, sin 2 > tg 2. Рассуждая аналогично, получаем, что

sin 2 > ctg 2, sin 3 > tg 3, sin 4 < tg 4, cos 6 > tg 6 и т.д.

Сравним sin 1 и tg 1, cos 1 и сtg 1.

Для положительных чисел при делении некоторого числа на число, меньшее 1, его значение увеличивается. Косинус и синус меньше единицы (за исключением частных случаев). Поэтому в первой четверти, где синус, косинус, тангенс и котангенс положительны, тангенс любого угла больше синуса этого угла, котангенс — больше  косинуса. Отсюда,

sin 1 < tg 1

cos 1 < сtg 1.

Сравниваем cos 1 и tg 1.

При сравнении отрицательных чисел сначала сравниваем их модули. Из отрицательных чисел больше то, модуль которого меньше.

Сравним cos 2 и tg 2.

Аналогично, sin 5 > tg 5, sin 6> tg 6, cos 2 > ctg 2.