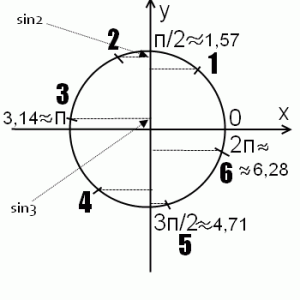
Сравнить значения ctg 2 и tg 2, ctg 1 и tg 1, ctg 3 и tg 3, ctg 4 и tg 4 можно с помощью единичной окружности, не прибегая к помощи калькулятора и таблиц.
Легче всего это сделать с помощью оценки значений косинусов (cos 1, c0s 2, ...) и синусов (sin 1, sin2, …) на единичной окружности.
Поскольку
![]()
то значения ctg 2 и tg 2, ctg 1 и tg 1, ctg 3 и tg 3, ctg 4 и tg 4, ctg 5 и tg 5, ctg 6 и tg 6 сравниваем, исходя из следующих рассуждений: если косинус больше синуса, то, соответственно, котангенс больше тангенса, и наоборот. Точнее, речь идет о модулях синуса и косинуса и модулях тангенса и котангенса.
Разбираем на примерах. cos 1 < sin 1, следовательно,
![]()
так как делим меньшее число на большее. А для тангенса — наоборот:
![]()
![]()
Поскольку во второй координатной четверти тангенс и котангенс отрицательные, то
![]()
Для ctg 3 и tg 3 все наоборот, поскольку модуль cos 3 меньше модуля sin 3, для отрицательных значений tg 3 и ctg 3 это означает, что ctg 3 < tg 3.
В третьей четверти тангенс и котангенс положительны, поэтому
![]()
В четвертой четверти, где тангенс и котангенс отрицательны:
![]()
![]()