Узнать ещё

Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.

 

 

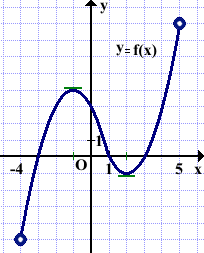
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.

Решение:

Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.

На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.

Ответ: 2.

Теперь рассмотрим аналогичное задание, в котором дан график производной функции.

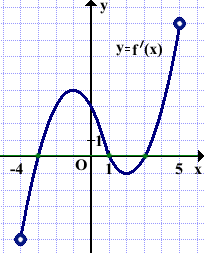2)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.

Решение:

Прямые y=k₁x+b₁ y=k₂x+b₂ параллельны, если их угловые коэффициенты равны: k₁=k₂.

y=12=0x+12, ⇒k₁=0.

Угловой коэффициент касательной равен значению производной в точке касания: k₂=f'(x_o).

Значит, ищем точки, в которых значение производной равно нулю.

Таких точек три (с абсциссами x=-3, x=1 и x=3).

Ответ: 3.

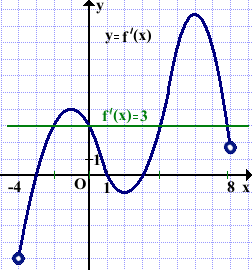3)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=3x-11 или совпадает с ней.

Решение:

y=3x-12, ⇒k₁=3.

Прямые параллельны, если k₁=k₂.

k₂=f'(x_o).

Поэтому ищем точки, в которых значение производной равно 3.

Таких точек в данном примере четыре.

Ответ: 4.

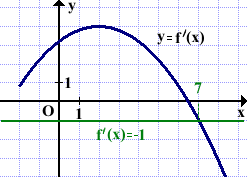4)На рисунке изображён график производной функции f(x). Найти абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=4-x или совпадает с ней.

Решение:

y=4-x,⇒k₁=-1.

Прямые параллельны, если k₁=k₂.

Прямые параллельны, если k₁=k₂.

k₂=f'(x_o).

Ищем точку, в которой значение производной равно -1.  Абсцисса этой точки x_o=7.

Ответ: 7.