« »

Рубрика: Легкое решение

Найти котангенс арксинуса

Если воспользоваться определениями синуса, котангенса в прямоугольном треугольнике, определением арксинуса и теоремой Пифагора, найти котангенс арксинуса ctg (arcsin x) очень легко.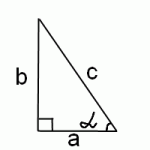По определению арксинуса, арксинус икса — это такое число альфа, синус которого равен x:

    \[\arcsin x = \alpha , \Rightarrow \sin \alpha = x.\]

Но синус — это отношение противолежащего катета к гипотенузе, то есть в нашем случае

    \[\sin \alpha = \frac{b}{c}.\]

А нам нужно найти котангенс этого же угла. Поскольку котангенс равен отношению прилежащего катета к противолежащему:

    \[ctg\alpha = \frac{a}{b},\]

остается найти прилежащий катет a. По теореме Пифагора

    \[a = \sqrt {{c^2} - {b^2}} .\]

Отсюда искомое значение котангенса арксинуса

    \[ctg(\arcsin x) = \frac{{\sqrt {{c^2} - {b^2}} }}{b}\]

где

    \[x = \frac{b}{c}.\]

Примеры.

1) Найти ctg (arcsin (3/5)).

Рассуждаем так же. Арксинус 3/5 — это такое число α, что sinα=3/5. Поскольку синус в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, то противолежащий катет b=3, гипотенуза с=5. Мы ищем котангенс этого же угла альфа, а котангенс равен отношение прилежащего катета к противолежащему. Прилежащий катет a находим по теореме Пифагора:

    \[a = \sqrt {{5^2} - {3^2}} = 4, \Rightarrow ctg(\arcsin \frac{3}{5}) = \frac{4}{3}.\]

2) Найти ctg (arcsin (1/3)).

arcsin (1/3)=α, значит sinα = 1/3, откуда противолежащий катет b=1, гипотенуза c=3. По теореме Пифагора, прилежащий катет a:

    \[a = \sqrt {{3^2} - {1^2}} = \sqrt 8 = 2\sqrt 2 \]

Так как ctgα равен отношению прилежащего катета к противолежащему, то

    \[ctg(\arcsin \frac{1}{3}) = \frac{{2\sqrt 2 }}{1} = 2\sqrt {2.} \]

Ваш отзыв , 18 Авг 2012

Ваш отзыв